题目内容
(本小题满分12分)
已知函数f(x)=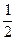 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),
(1)求f(x)的单调区间;(2)若x∈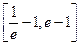 时,f(x)<m恒成立,求m的取值范围.?
时,f(x)<m恒成立,求m的取值范围.?
已知函数f(x)=
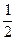 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),(1)求f(x)的单调区间;(2)若x∈
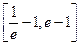 时,f(x)<m恒成立,求m的取值范围.?
时,f(x)<m恒成立,求m的取值范围.?解:解析:(1)∵f(x)=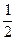 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),
∴f′(x)=(1+x)-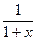 =
=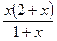 (x>-1).
(x>-1).
∴f(x)在(0,+∞)上单调递增,在(-1,0)上单调递减.
(2)令f′(x)=0,即x=0,则
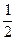 (1+x)2-ln(1+x),
(1+x)2-ln(1+x),∴f′(x)=(1+x)-
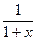 =
=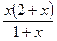 (x>-1).
(x>-1).∴f(x)在(0,+∞)上单调递增,在(-1,0)上单调递减.
(2)令f′(x)=0,即x=0,则
| x | 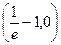 | 0 | (0,e-1) |
| f′(x) | - | 0 | + |
| f(x) |  ? ? | 极小值 |  ? ? |
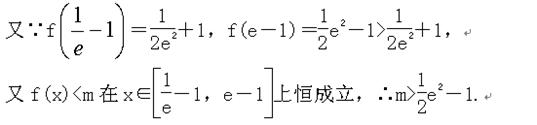 略
略
练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
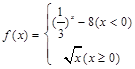 ,若f(a)>1,则实数a的取值范围是( )
,若f(a)>1,则实数a的取值范围是( )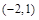
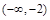 ∪
∪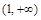
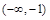 ∪(0,+∞)
∪(0,+∞)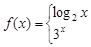
 ,则
,则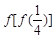 的值是( )
的值是( )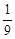

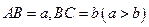 ,在AB、AD、CD、CB上分别
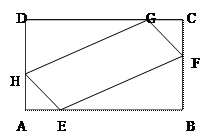
,在AB、AD、CD、CB上分别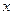 ,
,
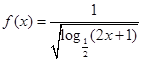 ,则
,则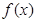 的定义域为( )
的定义域为( )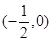
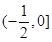
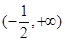
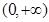
 ,则
,则 = .
= .  2+(K-1)x+3是偶函数,则f(x)的递减区间是
2+(K-1)x+3是偶函数,则f(x)的递减区间是 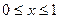 时,函数
时,函数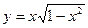 的最大值为
的最大值为 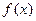 的定义域为[0,1],则
的定义域为[0,1],则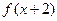 的定义域为 ;
的定义域为 ;