题目内容
2.下列结论中.正确的个数是3①若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,则存在实数x,y,使$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$
②若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$不共面,则不存在实数x,y,使$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$
③若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,$\overrightarrow{b}$,$\overrightarrow{c}$不共线,则存在实数x,y,使$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$
④若$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$则a,$\overrightarrow{b}$,$\overrightarrow{c}$共面.
分析 ①举例说明$\overrightarrow{b}$,$\overrightarrow{c}$共线,且$\overrightarrow{a}$与$\overrightarrow{b}$、$\overrightarrow{c}$不共线时,命题不成立;
②根据空间向量的共面定理以及逆否命题与原命题的真假性相同,即可判断命题正确;
③举例说明$\overrightarrow{a}$=$\overrightarrow{0}$与$\overrightarrow{b}$,$\overrightarrow{c}$共面,命题成立;
④根据空间向量的共面定理,得出命题正确.
解答 解:对于①,向量$\overrightarrow{b}$,$\overrightarrow{c}$共线,且$\overrightarrow{a}$与$\overrightarrow{b}$、$\overrightarrow{c}$不共线时,不存在实数x,y,使$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$,∴①错误;
对于②,根据空间向量的共面定理,结合逆否命题与原命题的真假性,得:
$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$不共面时,不存在实数x,y,使$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$,∴②正确;
对于③,若$\overrightarrow{a}$=$\overrightarrow{0}$时,与$\overrightarrow{b}$、$\overrightarrow{c}$共面,且$\overrightarrow{b}$,$\overrightarrow{c}$不共线,则存在实数x=y=0,使$\overrightarrow{a}$=0•$\overrightarrow{b}$+0•$\overrightarrow{c}$=$\overrightarrow{0}$,∴③正确;
对于④,根据空间向量的共面定理得,当$\overrightarrow{a}$=x$\overrightarrow{b}$+y$\overrightarrow{c}$时,$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面,∴④正确.
综上,正确的命题是②③④.
故答案为:3.
点评 本题考查了空间向量的基本概念问题,解题时应理解空间向量的基本定理,是基础题目.

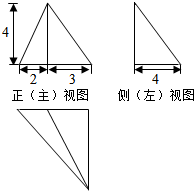
| A. | $\sqrt{61}$ | B. | $\sqrt{41}$ | C. | 2$\sqrt{5}$ | D. | 5 |
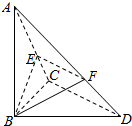 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}=λ(0<λ<1)$.
已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且$\frac{AE}{AC}=\frac{AF}{AD}=λ(0<λ<1)$.