题目内容
14.利用图象解不等式:(1)sin2x<-$\frac{1}{2}$;
(2)cos$\frac{x}{4}$≥$\frac{\sqrt{2}}{2}$.
分析 正确作出正弦、余弦函数的图象,根据图象,即可得出结论.
解答 解:(1)由图象可得2kπ+$\frac{7π}{6}$<2x<2kπ+$\frac{11π}{6}$,k∈z,
解得$\frac{7π}{12}$+kπ<x<$\frac{11π}{12}$+kπ,故不等式的解集为($\frac{7π}{12}$+kπ,$\frac{11π}{12}$+kπ),k∈z;
(2)由图象可得2kπ-$\frac{π}{4}$≤$\frac{x}{4}$≤2kπ+$\frac{π}{4}$,k∈z,
解得-π+4kπ≤x≤π+4kπ,故不等式的解集为[-π+4kπ,π+4kπ],k∈z;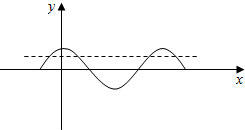
点评 本题考查正弦、余弦函数的单调性、定义域和值域,正确作出图象,由此求得不等式的解集是关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
4.已知两直线l1:(a-1)x-3y-10=0,l2:(a+1)x+y+3=0互相平行,则a=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
9.集合A={(x,y)|x-y+4≥0},B={(x,y)|y≥x(x-2)},则集合A∩B的所有元素组成的图形的面积是( )
| A. | $\frac{43}{2}$ | B. | $\frac{55}{2}$ | C. | $\frac{125}{6}$ | D. | 22 |
4.y=cos($\frac{π}{3}$-2x)的增区间为( )
| A. | [2kπ-π,2kπ],k∈Z | B. | [2kπ,2kπ+π],k∈Z | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2}{3}$π],k∈Z |
 如图所示,在△ABC中,点M是BC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点N在AC上,且AN=2NC,AM与BN相交于点P,AP=λAM,求
如图所示,在△ABC中,点M是BC的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点N在AC上,且AN=2NC,AM与BN相交于点P,AP=λAM,求