Question

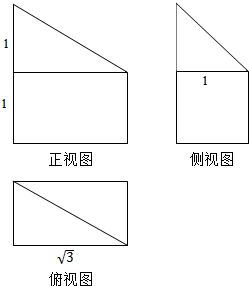
10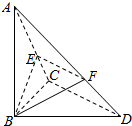．已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且$\frac{AE}{AC}=\frac{AF}{AD}=λ（0＜λ＜1）$．
（1）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（2）是否存在λ∈（0，1），使平面BEF⊥平面ACD？若存在，求出λ的值；若不存在，请说明理由．

Answer 1

分析 （1）由已知推导出AB⊥CD，CD⊥BC，从而CD⊥平面ABC，由此能证明不论λ为何值恒有平面BEF⊥平面ABC．
（2）由已知推导出BE⊥AC，由AB²=AE•AC，得当$λ=\frac{6}{7}$时，平面BEF⊥平面ACD．

解答 证明：（1）∵AB⊥平面BCD，∴AB⊥CD．
∵CD⊥BC，且AB∩BC=B，∴CD⊥平面ABC．
又∵$\frac{AE}{AC}=\frac{AF}{AD}=λ（0＜λ＜1）$，
∴不论λ为何值，恒有EF∥CD，
∴EF⊥平面ABC，EF?平面BEF，
∴不论λ为何值恒有平面BEF⊥平面ABC．
解：（2）由（1）知，BE⊥EF，
又平面BEF⊥平面ACD，
∴BE⊥平面ACD，∴BE⊥AC．
∵BC=CD=1，∠BCD=90°，∠ADB=60°，
∴$BD=\sqrt{2}，AB=\sqrt{2}tan{60°}=\sqrt{6}$，
∴$AC=\sqrt{A{B^2}+B{C^2}}=\sqrt{7}$
由AB²=AE•AC 得$AE=\frac{6}{{\sqrt{7}}}$，∴$λ=\frac{AE}{AC}=\frac{6}{7}$．
故当$λ=\frac{6}{7}$时，平面BEF⊥平面ACD．

点评 本题考查面面垂直的证明，考查使得面面垂直的两线段比值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．