题目内容
【题目】如图,在三陵锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点.
的中点.
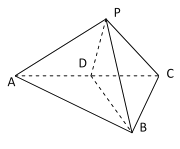
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为锐角,且棱锥
的平面角为锐角,且棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据等腰三角形三线合一,可证明线线垂直,再根据线面垂直判定定理,即可证明;
(2)根据题意,点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在射线
在射线![]() 上,再根据锥体体积公式可知
上,再根据锥体体积公式可知![]() ,由线面垂直的判定定理,可证
,由线面垂直的判定定理,可证![]() 平面
平面![]() ,则建系:以
,则建系:以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,利用空间向量法,求线面角.
轴建立空间直角坐标系,利用空间向量法,求线面角.
(1)
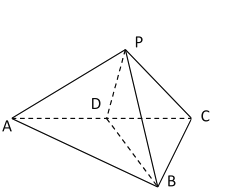
证明:∵![]() ,
,![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
又![]() 为等边三角形,
为等边三角形,![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)由(1)知点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,又二面角
上,又二面角![]() 的平面角为锐角,∴
的平面角为锐角,∴![]() 在射线
在射线![]() 上,
上,![]() ,
,![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,即
,即![]() 为
为![]() 中点,取
中点,取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 两两互相垂直,
两两互相垂直,
以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
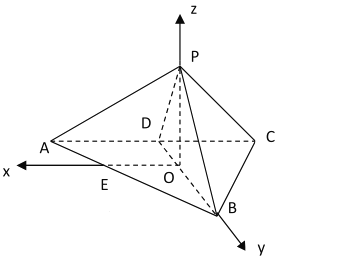
则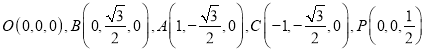
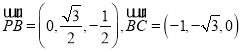
设平面![]() 的法向量为
的法向量为![]()
由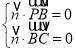 得
得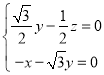
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又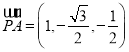 ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则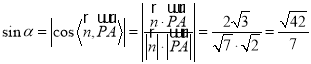 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】随着小汽车的普及,“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,他需要通过四个科目的考试,其中科目二为场地考试.在一次报名中,每个学员有5次参加科目二考试的机会(这5次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试;若5次都没有通过,则需重新报名),其中前2次参加科目二考试免费,若前2次都没有通过,则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计,得到下表:
考试情况 | 男学员 | 女学员 |
第1次考科目二人数 | 1200 | 800 |
第1次通过科目二人数 | 960 | 600 |
第1次未通过科目二人数 | 240 | 200 |
若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率,且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)若这对夫妻前2次参加科目二考试均没有通过,记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.