题目内容
(本小题满分1 2分)
甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子,乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.
(1)若甲在自己的箱子里任意取球,取后不放回,每次只取一球,直到取得红球为止,求甲取球次数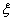 的数学期望;
的数学期望;
(2)若甲、乙两人各自从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜,这个游戏规则公平吗?请说明理由.
练习册系列答案
相关题目
题目内容
(本小题满分1 2分)
甲有一个放有3个红球、2个白球、1个黄球共6个球的箱子,乙也有一个放有3个红球、2个白球、1个黄球共6个球的箱子.
(1)若甲在自己的箱子里任意取球,取后不放回,每次只取一球,直到取得红球为止,求甲取球次数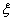 的数学期望;
的数学期望;
(2)若甲、乙两人各自从自己的箱子里任取一球比颜色,规定同色时为甲胜,异色时为乙胜,这个游戏规则公平吗?请说明理由.