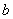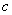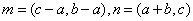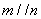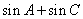题目内容
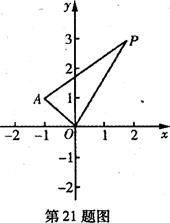
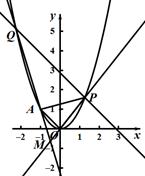
(本小题满分1 2分)在平面直角坐标系xOy中,已知点A(一1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
(I)求点P的轨迹C的方程;
(Ⅱ)若Q是轨迹C上异于点P的一个点,且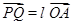 ,直线OP与QA交于点M,试探究:点M的横坐标是否为定值?并说明理由.
,直线OP与QA交于点M,试探究:点M的横坐标是否为定值?并说明理由.
【答案】
解:(Ⅰ)设点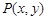 为所求轨迹上的任意一点,则由
为所求轨迹上的任意一点,则由 得
得
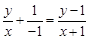 ,·························· 2分
,·························· 2分
整理得轨迹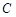 的方程为
的方程为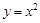 (
(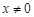 且
且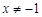 ),…4分
),…4分
(Ⅱ)(方法一)设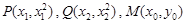 ,
,
由 可知直线
可知直线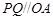 ,则
,则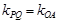 ,
,
故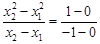 ,即
,即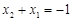 ,…………………6分
,…………………6分
由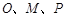 三点共线可知,
三点共线可知, 与
与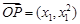 共线,
共线,
∴ 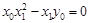 ,
,
由(Ⅰ)知 ,故
,故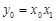 ,··················· 8分
,··················· 8分
同理,由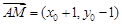 与
与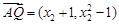 共线,
共线,
∴ 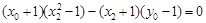 ,即
,即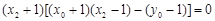 ,
,
由(Ⅰ)知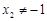 ,故
,故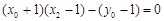 ,·········· 10分
,·········· 10分
将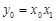 ,
,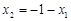 代入上式得
代入上式得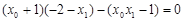 ,
,
整理得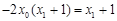 ,
,
由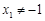 得
得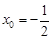 ,即点M的横坐标为定值
,即点M的横坐标为定值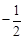 .·········· 12分
.·········· 12分
(方法二)
设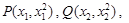
由 可知直线
可知直线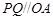 ,则
,则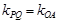 ,
,
故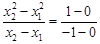 ,即
,即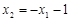 ,················· 6分
,················· 6分
∴直线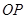 方程为:
方程为: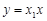 ①;·················· 8分
①;·················· 8分
直线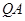 的斜率为:
的斜率为: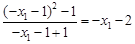 ,
,
∴直线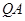 方程为:
方程为: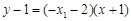 ,即
,即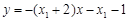 ②;· 10分
②;· 10分
联立①②,得 ,∴点
,∴点 的横坐标为定值
的横坐标为定值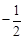 .·········· 12分
.·········· 12分
【解析】略

练习册系列答案
相关题目
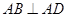 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD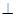 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.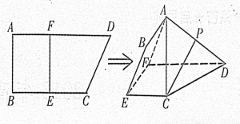
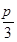 ,S△ABC=6
,S△ABC=6
 (Ⅰ)求
(Ⅰ)求