题目内容
若点O和点F(﹣2, 0)分别是双曲线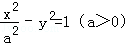 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则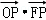 的取值范围为
的取值范围为
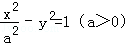 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则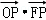 的取值范围为
的取值范围为A.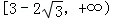 | B.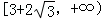 |
C.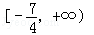 | D.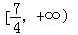 |
B
试题分析:根据题意,设点P(m,n),则可知
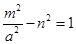 ,同时满足
,同时满足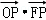 =
=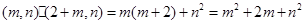 ,由于
,由于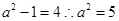 ,则可知c=2,
,则可知c=2,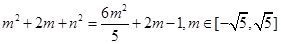 ,那么结合二次函数的性质可知,数量积的范围是
,那么结合二次函数的性质可知,数量积的范围是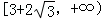 ,故选B.
,故选B.点评:解决的关键是根据通过向量的坐标表示来得到数量积的表达式,属于基础题。

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
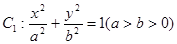 过点
过点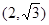 ,且它的离心率
,且它的离心率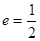 .直线
.直线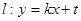 与椭圆
与椭圆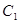 交于
交于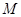 、
、 两点.
两点.
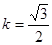 时,求证:
时,求证: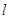 与圆
与圆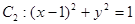 相切,椭圆上一点
相切,椭圆上一点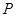 满足
满足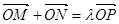 ,求实数
,求实数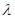 的取值范围.
的取值范围.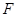 是椭圆
是椭圆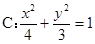 的右焦点,定点A
的右焦点,定点A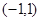 ,M是椭圆上的动点,则
,M是椭圆上的动点,则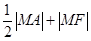 的最小值为 .
的最小值为 . 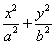 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为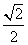 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(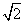 +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 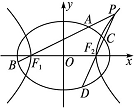
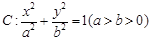 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为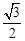 .
.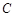 的标准方程;
的标准方程;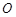 的直线
的直线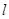 与椭圆
与椭圆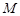 、
、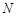 ,且直线
,且直线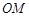 、
、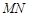 、
、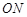 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△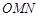 面积的取值范围.
面积的取值范围.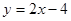 与抛物线
与抛物线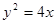 交于
交于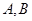 两点.
两点.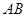 的长;(2)若抛物线
的长;(2)若抛物线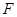 ,求
,求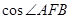 的值.
的值.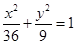 的弦被点
的弦被点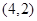 平分,则此弦所在的直线方程是 ( )
平分,则此弦所在的直线方程是 ( )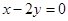
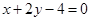
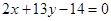
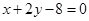
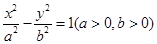 与椭圆
与椭圆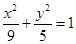 有相同的焦点
有相同的焦点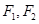 ,且该双曲线
,且该双曲线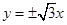 .
.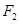 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点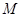 、
、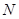 ,
,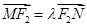 ,当
,当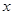 轴上的点
轴上的点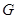 满足
满足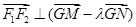 时,求点
时,求点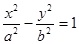 (a>0,b>0) 的焦点到渐近线的距离是a,则双曲线的离心率的值是 .
(a>0,b>0) 的焦点到渐近线的距离是a,则双曲线的离心率的值是 .