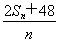Question

若数列{an}满足an＋1＝an＋an＋2(n∈N*)，则称数列{an}为“凸数列”．

(1)设数列{an}为“凸数列”，若a1＝1，a2＝－2，试写出该数列的前6项，并求出前6项之和；

(2)在“凸数列”{an}中，求证：an＋3＝－an，n∈N*；

(3)设a1＝a，a2＝b，若数列{an}为“凸数列”，求数列前2011项和S2011.

 

Answer 1

（1）S6＝0（2）见解析（3）a

【解析】(1)解：a1＝1，a2＝－2，a3＝－3，a4＝－1，a5＝2，a6＝3，故S6＝0.

(2)证明：由条件得所以an＋3＝－an.

(3)解：由(2)的结论得an＋6＝－an＋3＝an，即an＋6＝an.

a1＝a，a2＝b，a3＝b－a，a4＝－a，a5＝－b，a6＝a－b，∴S6＝0.

由(2)得S6n＋k＝Sk，n∈N*，k＝1，…，6，

故S2011＝S335×6＋1＝a1＝a.