题目内容
已知函数f(x)=mx+3,g(x)=x2+2x+m.
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1,若|G(x)|在[-1,0]上是减函数,求实数m的取值范围.
(1)见解析(2)m≤0或m≥2
【解析】(1)证明:f(x)-g(x)=(mx+3)-(x2+2x+m)=-x2+(m-2)x+(3-m).
由Δ1=(m-2)2+4(3-m)=m2-8m+16=(m-4)2≥0,知函数f(x)-g(x)必有零点.
(2)【解析】
|G(x)|=|-x2+(m-2)x+(2-m)|=|x2-(m-2)x+(m-2)|,
Δ2=(m-2)2-4(m-2)=(m-2)(m-6),
①当Δ2≤0,即2≤m≤6时,|G(x)|=x2-(m-2)x+(m-2),
若|G(x)|在[-1,0]上是减函数,则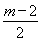 ≥0,即m≥2,所以2≤m≤6时,符合条件.
≥0,即m≥2,所以2≤m≤6时,符合条件.
②当Δ2>0,即m<2或m>6时,
若m<2,则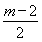 <0,要使|G(x)|在[-1,0]上是减函数,则
<0,要使|G(x)|在[-1,0]上是减函数,则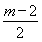 ≤-1且G(0)≤0,所以m≤0;
≤-1且G(0)≤0,所以m≤0;
若m>6,则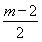 >2,要使|G(x)|在[-1,0]上是减函数,则G(0)≥0,所以m>6.
>2,要使|G(x)|在[-1,0]上是减函数,则G(0)≥0,所以m>6.
综上,m≤0或m≥2.

练习册系列答案
相关题目