题目内容
已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1)求a1,a2的值;
(2)设a1>0,数列 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
(1)a1=0,a2=0或a1=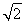 +1,a2=
+1,a2=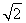 +2或a1=1-
+2或a1=1-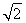 ,a2=2-
,a2=2-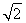 .(2)n=7时,Tn取得最大值,T7=7-
.(2)n=7时,Tn取得最大值,T7=7- lg2.
lg2.
【解析】(1)取n=1时,a2a1=S2+S1=2a1+a2,①
取n=2时,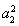 =2a1+2a2.②由②-①得,a2(a2-a1)=a2.③
=2a1+2a2.②由②-①得,a2(a2-a1)=a2.③
若a2=0,由①知a1=0;若a2≠0,由③知a2-a1=1.④
由①④解得a1= +1,a2=2+
+1,a2=2+ 或a1=1-
或a1=1-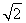 ,a2=2-
,a2=2- .
.
综上所述,a1=0,a2=0或a1=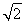 +1,a2=
+1,a2=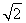 +2或a1=1-
+2或a1=1-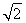 ,a2=2-
,a2=2-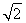 .
.
(2)当a1>0时,a1=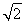 +1,a2=
+1,a2= +2.
+2.
n≥2时,有(2+ )an=S2+Sn,(2+
)an=S2+Sn,(2+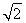 )an-1=S2+Sn-1,
)an-1=S2+Sn-1,
∴(1+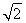 )an=(2+
)an=(2+ )an-1,即an=
)an-1,即an= an-1(n≥2),
an-1(n≥2),
∴an=a1( )n-1=(
)n-1=(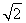 +1)(
+1)(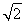 )n-1.令bn=
)n-1.令bn= =1-
=1-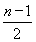 lg2,
lg2,
故{bn}是递减的等差数列,从而b1>b2>…>b7=lg >lg1=0,
>lg1=0,
n≥8时,bn≤b8= lg
lg <
< lg1=0,故n=7时,Tn取得最大值,T7=7-
lg1=0,故n=7时,Tn取得最大值,T7=7- lg2
lg2

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目