题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 作与
作与![]() 轴不重合的直线
轴不重合的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,
,![]() 分别交直线
分别交直线![]() 于,
于,![]() ,
,![]() 两点,若直线
两点,若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试问:
,试问:![]() 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为定值
为定值![]() ,理由见解析
,理由见解析
【解析】
(1)结合椭圆离心率、![]() 的面积、
的面积、![]() 列方程组,解方程组求得
列方程组,解方程组求得![]() ,由此求得椭圆的标准方程.
,由此求得椭圆的标准方程.
(2)当直线![]() 斜率不存在时,求得
斜率不存在时,求得![]() 两点的坐标,由此求得直线
两点的坐标,由此求得直线![]() 的方程,进而求得
的方程,进而求得![]() 两点的坐标,由此求得
两点的坐标,由此求得![]() ,
,![]() ,求得
,求得![]() .当直线
.当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 方程为
方程为![]() ,联立直线的方程和椭圆方程,写出韦达定理,求得直线
,联立直线的方程和椭圆方程,写出韦达定理,求得直线![]() 的方程,进而求得
的方程,进而求得![]() 两点的坐标,由此求得
两点的坐标,由此求得![]() ,
,![]() ,结合韦达定理计算
,结合韦达定理计算![]() .由此证得
.由此证得![]() 为定值
为定值![]() .
.
(1)由题意得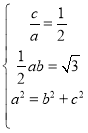 ,
,
解得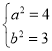 ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)知![]() ,
,![]() ,
,
①当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() 方程为
方程为![]() ,
,
联立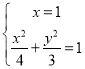 ,得
,得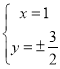 ,
,
不防设![]() ,
,![]() ,
,
则直线![]() 方程为
方程为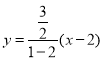 ,
,
令![]() ,得
,得![]() ,则
,则![]() ,
,
此时,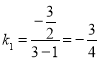 ,
,
同理![]() ,
,
所以![]() ,
,
②当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 方程为
方程为![]() ,
,
联立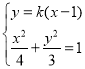 ,得
,得![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
直线![]() 方程为
方程为![]() ,
,
令![]() ,得
,得![]() ,则
,则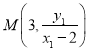 ,
,
同理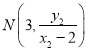 ,
,
所以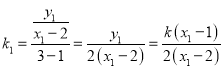 ,
,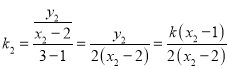 ,
,
所以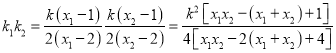
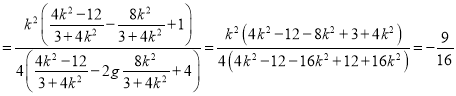
综上所述,![]() 为定值
为定值![]() .
.

练习册系列答案
相关题目
【题目】某初级中学共有学生2000名,各年级男生女生人数如表: 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
(1)求x的值.
(2)现用分层抽样法在全校抽取48名学生,问应在初三年级学生中抽取多少名?
(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.