题目内容
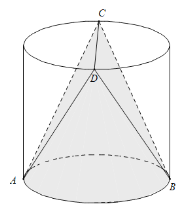
【题目】已知空间几何体
是由圆柱切割而成的阴影部分构成，其中
，
为下底面圆直径的两个端点，
，
为上底面圆直径的两个端点，且
，圆柱底面半径是1，高是2，则空间几何体可以无缝的穿过下列哪个图形（ ）
A.椭圆B.等腰直角三角形C.正三角形D.正方形
【答案】D
【解析】
由题意可知
，且该几何体的高也是2，A中直接根据椭圆的几何性质可知A不符合题意；B、C中设
为
的中点，连接
，
，易得
既不是直角三角形，也不是正三角形，均不符合题意；D中边长为2的正方形恰好和以
为直径的圆相切，符合题意．
解：由题意可知，且该几何体的高也是2，
A中，若椭圆的长轴长为2，短轴长小于2，则几何体无法穿过，若椭圆的短轴长为2，长轴长大于2，则几何体穿过时有缝隙，均不符合题意；
B中，设为的中点，连接，，则易证
为二面角
的平面角，易求得
，而
，则不是直角三角形，故B不符合题意；
C中，由B中结论，
，不是正三角形，故C不符合题意；
D中，由题意，边长为2的正方形恰好和以为直径的圆相切，故D符合题意；
故选：D．
练习册系列答案
相关题目
