题目内容
(本小题14分)已知直线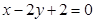 经过椭圆
经过椭圆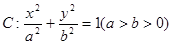 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆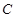 的右顶点为
的右顶点为 ,点
,点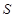 是椭圆
是椭圆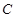 上位于
上位于 轴上方的动点,直线
轴上方的动点,直线 与直线
与直线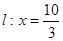 分别交于
分别交于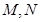 两点。
两点。
(I)求椭圆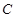 的方程;
的方程;
(Ⅱ)求线段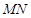 的长度的最小值;
的长度的最小值;
(Ⅲ)当线段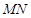 的长度最小时,在椭圆
的长度最小时,在椭圆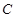 上是否存在这样的点
上是否存在这样的点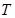 ,使得
,使得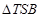 的面积为
的面积为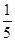 ?若存在,确定点
?若存在,确定点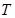 的个数,若不存在,说明理由。
的个数,若不存在,说明理由。
(I) ;(Ⅱ)
;(Ⅱ)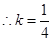 时,线段
时,线段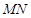 的长度取最小值
的长度取最小值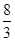
(Ⅲ)当线段MN的长度最小时,在椭圆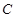 上存在2个不同的点
上存在2个不同的点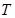 ,使得
,使得 的面积为
的面积为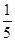
解析试题分析:(1)由已知得,椭圆C的左顶点为A(-2,0),上顶点为D(0,1,由此能求出椭圆C的方程.(2)设直线AS的方程为y=k(x+2),从而M(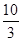 ,
,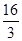 k).由题设条件可以求出N(
k).由题设条件可以求出N(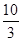 ,-
,-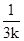 ),所以|MN|得到表示,再由均值不等式进行求解
),所以|MN|得到表示,再由均值不等式进行求解
(3)在第二问的基础上确定了直线BS的斜率得到直线方程,利用点到直线的距离得到l‘,然后得到分析方程组的解的个数即为满足题意的点的个数。
解:(I)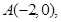
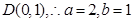 ;故椭圆
;故椭圆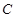 的方程为
的方程为
(Ⅱ)直线AS的斜率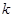 显然存在,且
显然存在,且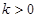 ,故可设直线
,故可设直线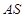 的方程为
的方程为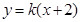 ,从而
,从而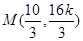
由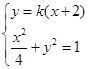 得
得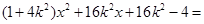 0
0
设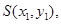 则
则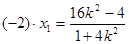 得
得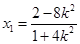 ,
,
从而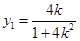 即
即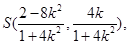 又
又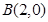
由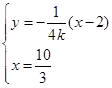 得
得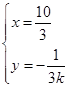
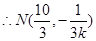 故
故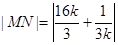
又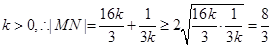
当且仅当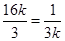 ,即
,即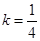 时等号成立。
时等号成立。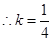 时,线段
时,线段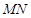 的长度取最小值
的长度取最小值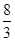
(Ⅲ)由(Ⅱ)可知,当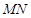 取最小值时,
取最小值时,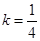
此时 的方程为
的方程为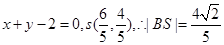
要使椭圆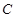 上存在点
上存在点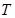 ,使得
,使得 的面积等于
的面积等于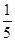 ,只须
,只须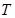 到直线
到直线 的距离等于
的距离等于 ,所以
,所以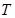 在平行于
在平行于 且与
且与 距离等于
距离等于 的直线
的直线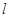 上。设直线
上。设直线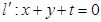
则由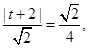 解得
解得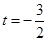 或
或
当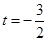 时,
时,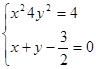 得
得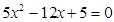 ,
, ,故有2个不同的交点;
,故有2个不同的交点;
当 时,
时,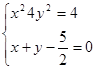 得
得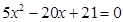 ,
,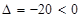 ,故没有交点;
,故没有交点;
综上:当线段MN的长度最小时,在椭圆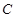 上存在2个不同的点
上存在2个不同的点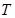 ,使得
,使得 的面积为
的面积为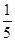
考点:本试题主要考查了椭圆与直线的位置关系,解题时要注意公式的灵活运用.
点评:解决该试题的关键是能利用椭圆的几何性质表述出|MN|,同时结合均值不等式求解最小值。

练习册系列答案
相关题目
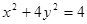 ,直线
,直线 :y=x+m
:y=x+m  的值;
的值; 的中心,而焦点是双曲线的顶点,求抛物线的方程.
的中心,而焦点是双曲线的顶点,求抛物线的方程.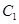 :
: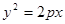 的准线经过双曲线
的准线经过双曲线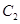 :
: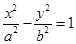 的左焦点,若抛物线
的左焦点,若抛物线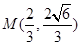 .
.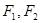 是双曲线
是双曲线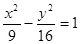 的两个焦点,点
的两个焦点,点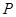 在双曲线上,且
在双曲线上,且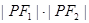
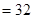 ,求证:
,求证: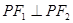
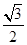 的椭圆
的椭圆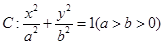 过点
过点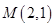 ,
,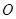 为坐标原点,平行于
为坐标原点,平行于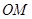 的直线
的直线 交椭圆于
交椭圆于 不同的两点
不同的两点 。
。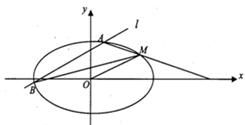
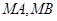 的斜率分别为
的斜率分别为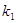 、
、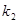 ,求证:
,求证: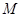 与直线
与直线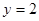 相切,且与定圆
相切,且与定圆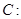
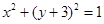 外切,求动圆圆心
外切,求动圆圆心 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 ,最小值为
,最小值为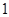 .
.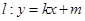 与椭圆
与椭圆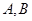 两点(
两点(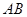 为直径的圆过椭圆
为直径的圆过椭圆 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.  ,F2(0,
,F2(0,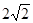 ),且离心率
),且离心率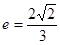 。
。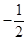 ,求直线l的斜率的取值范围。
,求直线l的斜率的取值范围。