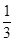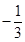题目内容
设α∈(0, ),β∈(
),β∈( ,
, ),且5
),且5 sinα+5cosα=8,
sinα+5cosα=8, sinβ+
sinβ+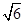 cosβ=2,则cos(α+β)的值为________.
cosβ=2,则cos(α+β)的值为________.
 ),β∈(
),β∈( ,
, ),且5
),且5 sinα+5cosα=8,
sinα+5cosα=8, sinβ+
sinβ+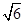 cosβ=2,则cos(α+β)的值为________.
cosβ=2,则cos(α+β)的值为________.-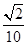
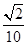
由5 sinα+5cosα=8得,sin(α+
sinα+5cosα=8得,sin(α+ )=
)=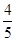 ,
,
∵α∈(0, ),∴cos(α+
),∴cos(α+ )=
)=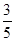 .
.
又β∈( ,
, ),由已知得sin(β+
),由已知得sin(β+ )=
)=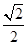 ,
,
∴cos(β+ )=-
)=-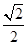 .
.
∴cos(α+β)=sin[ +(α+β)]=sin[(α+
+(α+β)]=sin[(α+ )+(β+
)+(β+ )]=sin(α+
)]=sin(α+ )cos(β+
)cos(β+ )+cos(α+
)+cos(α+ )sin(β+
)sin(β+ )=-
)=-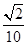 .
.
 sinα+5cosα=8得,sin(α+
sinα+5cosα=8得,sin(α+ )=
)=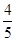 ,
,∵α∈(0,
 ),∴cos(α+
),∴cos(α+ )=
)=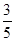 .
.又β∈(
 ,
, ),由已知得sin(β+
),由已知得sin(β+ )=
)=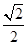 ,
,∴cos(β+
 )=-
)=-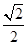 .
.∴cos(α+β)=sin[
 +(α+β)]=sin[(α+
+(α+β)]=sin[(α+ )+(β+
)+(β+ )]=sin(α+
)]=sin(α+ )cos(β+
)cos(β+ )+cos(α+
)+cos(α+ )sin(β+
)sin(β+ )=-
)=-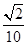 .
.
练习册系列答案
相关题目

 ,sin(
,sin( )=-
)=- sin
sin 则cos
则cos = _.
= _. ,tan
,tan =
= ,则cosβ的值为________.
,则cosβ的值为________. ,sin(
,sin( ,求
,求 的值.
的值. 中,其中
中,其中 为定点,
为定点, 为动点,
为动点, .
. 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和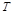 ,求
,求 的最大值。
的最大值。 =( )
=( )


 ( )
( )



 .
. ,
, ,则
,则 ( )
( )