题目内容
两圆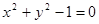 和
和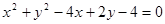 的位置关系是
的位置关系是
| A.内切 | B.相交 | C.外切 | D.外离 |
B
解析试题分析:根据题意,由于两圆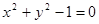 和
和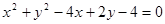 的圆心(0,0)和(2,-1),半径分别是1,3,那么可知圆心距为
的圆心(0,0)和(2,-1),半径分别是1,3,那么可知圆心距为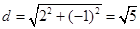 ,那么此数
,那么此数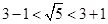 ,<小于半径和,大于半径差,因此是相交,故选B.
,<小于半径和,大于半径差,因此是相交,故选B.
考点:两圆的位置关系
点评:解决两圆的位置关系的判定,主要是考查了圆心距和半径的关系,然后结合关系式得到结论,要熟练掌握。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若抛物线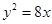 上一点
上一点 到其焦点的距离为
到其焦点的距离为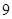 ,则点
,则点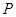 的坐标为( )
的坐标为( )
A.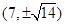 | B.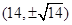 | C.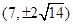 | D.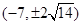 |
双曲线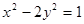 的右焦点的坐标为 ( )
的右焦点的坐标为 ( )
A.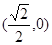 | B.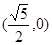 | C.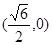 | D.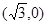 |
若直线mx- ny = 4与⊙O: x2+y2= 4没有交点,则过点P(m,n)的直线与椭圆 的交点个数是 ( )
的交点个数是 ( )
| A.至多为1 | B.2 | C.1 | D.0 |
已知F1,F2为双曲线C: 的左右焦点,点P在C上,
的左右焦点,点P在C上, ,则
,则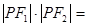 ( )
( )
| A. 2 | B. 4 | C. 6 | D. 8 |
当a为任意实数时,直线 恒过定点P,则过点P的抛物线的标准方程是( )
恒过定点P,则过点P的抛物线的标准方程是( )
A.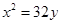 或 或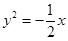 | B.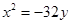 或 或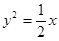 |
C.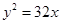 或 或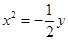  | D.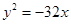 或 或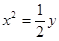 |
设 是曲线
是曲线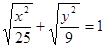 上的点,
上的点,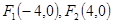 ,则( )
,则( )
A.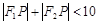 | B.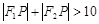 |
C.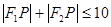 | D.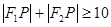 |
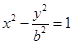 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线 ,若
,若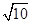 B.
B.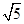 C.
C.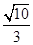 D.
D.