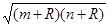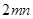题目内容
设P是双曲线=1(a>0 ,b>0)上的点,F1、F2是焦点,双曲线的离心率是,且∠F1PF2=90°,△F1PF2面积是9,则a + b=( )
| A.4 | B.5 | C.6 | D.7 |
D
解析试题分析:依题意,不妨设点P是双曲线右支上的点,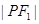 =m,
=m,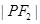 =n,那么
=n,那么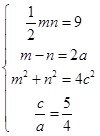 ,解得a=4,c=5,所以b=3,a+b=7,故选D。
,解得a=4,c=5,所以b=3,a+b=7,故选D。
考点:本题主要考查双曲线的定义及几何性质。
点评:中档题,本题利用数形结合思想,依题意布列方程组,通过求得a,b的值而得解。对学生的运算能力有较好考查。

练习册系列答案
相关题目
椭圆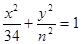 和双曲线
和双曲线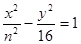 有相同的焦点,则实数
有相同的焦点,则实数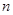 的值是 ( )
的值是 ( )
A.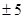 | B.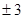 | C.5 | D.9 |
设双曲线 的虚轴长为2,焦距为
的虚轴长为2,焦距为 ,则双曲线的渐近线方程为( ).
,则双曲线的渐近线方程为( ).
A.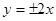 | B. | C.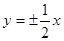 | D. |
设F1,F2分别是双曲线 的左、右焦点.若双曲线上存在点A,使
的左、右焦点.若双曲线上存在点A,使 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. | B. | C. | D.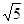 |
从抛物线 上任意一点
上任意一点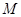 向圆
向圆 作切线
作切线 ,则切线长
,则切线长 的最小值为
的最小值为
A.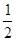 | B.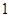 | C. | D.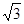 |
两圆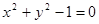 和
和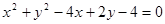 的位置关系是
的位置关系是
| A.内切 | B.相交 | C.外切 | D.外离 |

 与抛物线
与抛物线 相交于
相交于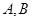 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若 ,则k的值为( )。
,则k的值为( )。



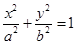 与
与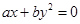 (
( >
>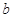 > 0 )的曲线大致是
> 0 )的曲线大致是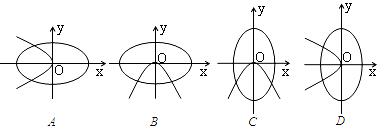
 为一个焦点的椭圆,近地点A距地面为
为一个焦点的椭圆,近地点A距地面为 千米,远地点B距地面为
千米,远地点B距地面为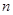 千米,地球半径为
千米,地球半径为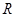 千米,则飞船运行轨道的短轴长为( )
千米,则飞船运行轨道的短轴长为( )