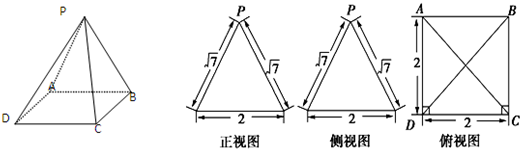
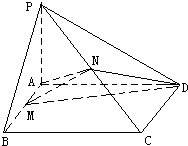
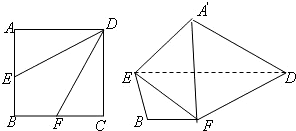
题目内容

（理科做）（1）证明：面APC⊥面BEF；
（2）求平面PBC与平面PCD夹角的余弦值．
证明：
(理)(1)连接EP、EC，由题可知
BP=BC=2
2
，
∴BF⊥PC，又△PAE≌△CDE，∴EP=EC，
∴EF⊥PC，且EF∩BF=F，
故PC⊥面BEF，又PC?面APC，
∴面APC⊥面BEF；
（2）在△PCD中作DG⊥PC交PC于点G，则DG=
PD•CD
PC
=
2×2
3
4
=
3
，
又由DG2=CD•PG得CG=1，
∴点G为CF的中点，取BC中点H，
连接GH、HD，则GH\mathop∥limits=BF，GH=1，
∴GH⊥PC，∠HGD为二面角的平面角，
Rt△CDH中可得HD=
6
，
∴COS∠HGD=
3+1-6
2×1×
3
=-
3
3
．
练习册系列答案
相关题目

四棱锥S-ABCD的底面ABCD是正方形，侧棱SC的中点E在底面内的射影恰好是正方形ABCD的中心O，顶点A在截面SBD内的射影恰好是△SBD的重心G．
（1）求直线SO与底面ABCD所成角的正切值；
（2）设AB=a，求此四棱锥过点C，D，G的截面面积．
一个四棱锥的三视图如图所示．

（1）求这个四棱锥的全面积及体积；
（2）求证：PA⊥BD；
（3）在线段PD上是否存在一点Q，使二面角Q-AC-D的平面角为30°？若存在，求
|DQ|
|DP|
的值；若不存在，说明理由．
如图，已知ABCD是矩形，PA⊥平面ABCD，M，N分别是AB，PC的中点，PA=2，PD=AB，且平面MND⊥平面PCD．
（1）求证：MN⊥AB；
（2）求二面角P-CD-A的大小；
（3）求三棱锥D-AMN的体积．
正三棱锥底面边长为a，侧棱与底面成角为60°，过底面一边作一截面使其与底面成30°的二面角，则此截面的面积为（　　）
A．
3
4
a2		B．
3
3
a2		C．
1
3
a2		D．
3
8
a2
正四棱柱ABCD-A1B1C1D1中，底面边长为a，侧棱AA1长为ka（k＞0），E为侧棱BB1的中点，记以AD1为棱，EAD1，A1AD1为面的二面角大小为θ．
（1）是否存在k值，使直线AE⊥平面A1D1E，若存在，求出k值；若不存在，说明理由；
（2）试比较tanθ与2
2
的大小．
如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E为棱AB的中点．
求：
（1）D1E与平面BC1D所成角的正弦值；
（2）二面角D-BC1-C的余弦值．
如图，在边长为2的正方形ABCD中，点E是AB的中点，点F是BC的中点，将△AED，△CDF分别沿DE，DF折起，使A，C两点重合于A′．

（1）求证：A′D⊥EF；
（2）求二面角A′-EF-D的正切值．
一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线，侧视图和俯视图全全等的等腰直角三角形，直角边长为2，直观图如图．
（1）求四棱锥P一ABCD的体积：
（2）求二面角C-PB-A大小；
（3）M为棱PB上的点，当PM长为何值时，CM⊥PA？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网