题目内容
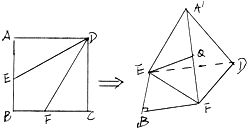
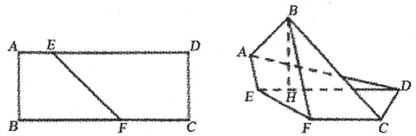
如图,边长为2的正方形ABCD中,点E、F分别是边AB、BC上的点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′.
(1)△A′EF恰好是正三角形且Q是A′F的中点,求证:EQ⊥平面A′FD
(2)当E、F分别是AB、BC的中点时,求二面角A′-EF-D的正弦值.
(1)△A′EF恰好是正三角形且Q是A′F的中点,求证:EQ⊥平面A′FD
(2)当E、F分别是AB、BC的中点时,求二面角A′-EF-D的正弦值.

(1)∵DA′⊥A′E,DA′⊥A′F,A′E∩A′F=A′,
∴DA′⊥面A′EF,
∴DA′⊥EQ,
又△A′EF为正三角形,Q′为A′F的中点,
∴EQ⊥A′F,A′F∩DA′,
∴EQ⊥面DA′F;
(2)∵E、F为AB、BC的中点,
∴A′E=A′F=1,ED=FD=
=
,EF=
=
,
取EF中点O,连接A′O,OD,则A′O⊥EF,DO⊥EF,
∴∠A′OD为二面角A′-EF-D平面角,
OD=
=
=
,A′O=
=
=
,
在△A′OD中,cos∠A′OD=
=
=
,
∴∠A′OD=arccos
,
故二面角A′-EF-D大小为arccos
.
∴DA′⊥面A′EF,
∴DA′⊥EQ,
又△A′EF为正三角形,Q′为A′F的中点,
∴EQ⊥A′F,A′F∩DA′,
∴EQ⊥面DA′F;
(2)∵E、F为AB、BC的中点,
∴A′E=A′F=1,ED=FD=
| AD2+AE2 |
| 5 |
| BE2+BF2 |
| 2 |
取EF中点O,连接A′O,OD,则A′O⊥EF,DO⊥EF,
∴∠A′OD为二面角A′-EF-D平面角,
OD=
| ED2-OE2 |
5-(
|
3
| ||
| 2 |
| A′E2-EO2 |
1-(
|
| ||
| 2 |
在△A′OD中,cos∠A′OD=
| A′O2+OD2-A′D2 |
| 2A′O•OD |
| ||||||||
2×
|
| 1 |
| 3 |
∴∠A′OD=arccos
| 1 |
| 3 |
故二面角A′-EF-D大小为arccos
| 1 |
| 3 |

练习册系列答案
相关题目

 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面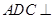 平面
平面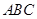 ,
, 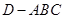 中,给出下列三个命题:
中,给出下列三个命题: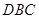 是等边三角形; ②
是等边三角形; ②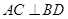 ;
; 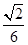 .
.