题目内容
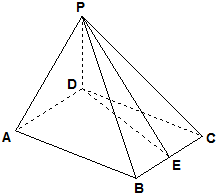
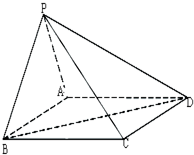
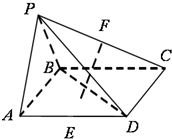
四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a.
(I)若M是底面ABCD的一个动点,且满足|MB|=|MS|,求点M在正方形ABCD内的轨迹;
(II)试问在线段SD上是否存在点E,使二面角C-AE-D的大小为60°?若存在,确定点E的位置;若不存在,请说明理由.

(I)若M是底面ABCD的一个动点,且满足|MB|=|MS|,求点M在正方形ABCD内的轨迹;
(II)试问在线段SD上是否存在点E,使二面角C-AE-D的大小为60°?若存在,确定点E的位置;若不存在,请说明理由.

(1)以D为原点,
、
、
的方向分别为x、y、z轴的正方向建立空间直角坐标系,
则B(a,a,0),S(0,0,a),…(2分)
设M(x,y,0),则由|MB|=|MS|得
=
…(4分)
化简得x+y-
=0,所以点M在正方形ABCD内的轨迹为△ACD平行于边AC的中位线.…(6分)
(2)假设存在,设
=λ
(0≤λ≤1),
=(0,a,0)为平面ADE的一个法向量…(8分)
设平面ACE的一个法向量为
=(x,y,z),则
•
=0,
•
=0
即
,取z=1,得
=(λ,λ,1),…(10分)
所以cos600=
=
,又0≤λ≤1,解得λ=
,
故在线段SD上存在点E,
=
,使二面角C-AE-D的大小为600.…(13分)
| DA |
| DC |
| DS |
则B(a,a,0),S(0,0,a),…(2分)
设M(x,y,0),则由|MB|=|MS|得
| (x-a)2+(y-a)2 |
| x2+y2+a2 |
化简得x+y-
| a |
| 2 |
(2)假设存在,设
| DE |
| DS |
| DC |
设平面ACE的一个法向量为
| n |
| n |
| EA |
| n |
| EC |
即
|
| n |
所以cos600=
|
| ||||
|
|
| |λ| | ||
|
| ||
| 2 |
故在线段SD上存在点E,
| DE |
| ||
| 2 |
| DS |

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目