题目内容
7.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2}+x,x≤1}\\{-lo{g}_{3}x,x>1}\end{array}\right.$,g(x)=|x-k|+|x-1|,若对任意的x1,x2∈R,都有f(x1)≤g(x2)成立,则实数k的取值范围为( )| A. | (-$∞,\frac{3}{4}$)∪($\frac{5}{4},+∞$) | B. | (-$∞,\frac{3}{4}$]∪[$\frac{5}{4},+∞$) | C. | [$\frac{3}{4},\frac{5}{4}$] | D. | ($\frac{3}{4},\frac{5}{4}$) |
分析 求出函数的最值,不等式有f(x1)≤g(x2)等价为有f(x)max≤g(x)min即可.
解答 解:当x≤1时,f(x)=-x2+x=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$≤$\frac{1}{4}$,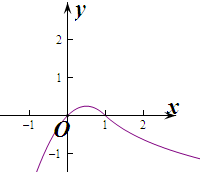
当x>1时,f(x)=-log3x<0,
则函数f(x)max=$\frac{1}{4}$,
g(x)=|x-k|+|x-1|≥|k-x+x-1|=|k-1|,
若对任意的x1,x2∈R,都有f(x1)≤g(x2)成立,
则|k-1|≥$\frac{1}{4}$,
即k-1≥$\frac{1}{4}$或k-1≤-$\frac{1}{4}$,
即k≥$\frac{5}{4}$或k≤$\frac{3}{4}$,
故选:B
点评 本题主要考查不等式恒成立问题,求出函数的最值是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
18.把长度为16的线段分成两段,各围成一个正方形,它们的面积和最小值为( )
| A. | 2 | B. | 4 | C. | 5 | D. | 8 |
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD,PD⊥底面ABCD.