题目内容
【题目】某物流公司专营从甲地到乙地的货运业务（货物全部用统一规格的包装箱包装），现统计了最近100天内每天可配送的货物量，按照可配送货物量T（单位：箱）分成了以下几组：
，
，
，
，
，
，并绘制了如图所示的频率分布直方图（同一组数据用该组数据的区间中点值作代表，将频率视为概率）.
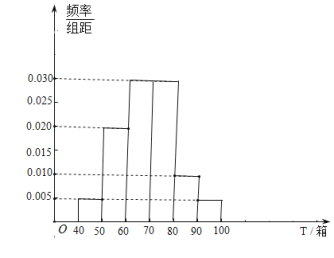
（1）该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的原因，并从这11天的数据中再抽出3天的数据进行财务分析，求这3天的数据中至少有2天的数据来自这一组的概率.
（2）由频率分布直方图可以认为，该物流公司每日的可配送货物量T（单位：箱）服从正态分布
，其中
近似为样本平均数.
（ⅰ）试利用该正态分布，估计该物流公司2000天内日货物配送量在区间
内的天数（结果保留整数）.
（ⅱ）该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一：直接发放奖金，按每日的可配送货物量划分为以下三级：
时，奖励50元；
，奖励80元；
时，奖励120元.
方案二：利用抽奖的方式获得奖金，其中每日的可配送货物量不低于时有两次抽奖机会，每日的可配送货物量低于时只有一次抽奖机会，每次抽奖的奖金及对应的概率分别为
奖金 | 50 | 100 |
概率 |
|
|
小张恰好为该公司装卸货物的一名员工，试从数学期望的角度分析，小张选择哪种奖励方案对他更有利？
附：若
，则
，
.
【答案】（1）
（2）（ⅰ）
天（ⅱ）小张选择方案二更有利
【解析】
（1）由分层抽样知识可知，这11天中前3组的数据分别有1个，4个，6个，即可求得相应的概率；
（2）（ⅰ）由
，可得
的值，得到日货物配送量在区间
内的天数；（ⅱ）由
，方案一，设小张每日可获得的奖金为
的可能取值，求得期望值；方案二，设小张每日可获得的奖金为
的所有可能取值，求得相应的概率，得出分布列，利用公式求得数学期望，比较两个期望值的大小，即可求解.
（1）由分层抽样知识可知，这11天中前3组的数据分别有1个，4个，6个，
所以至少有2天的数据来自
这一组的概率概率为
.
（2）（ⅰ）由题得
，
所以
.
故2000天内日货物配送量在区间内的天数为
.
（ⅱ）易知.
对于方案一，设小张每日可获得的奖金为元，则的可能取值为50，80，120，
其对应的概率分别为0.25，0.6，0.15，
故
.
对于方案二，设小张每日可获得的奖金为元，则的所有可能取值为50，100，150，200，
故
，
，
，
.
所以的分布列为
| 50 | 100 | 150 | 200 |
|
|
|
|
|
所以
.
因为
，
所以从数学期望的角度看，小张选择方案二更有利.
