题目内容
已知C:x2+y2=1和C1: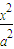 +
+ =1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.
=1 (a>b>0).试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点,与C外切,与C1内接的平行四边形?并证明你的结论.
【答案】分析:利用PQRS是与C外切,与C1内接的平行四边形,可得PQRS是菱形,于是OP⊥OQ,设出P,Q的坐标,在直角△POQ中,可得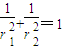 ,利用点在曲线上,即可求得结论.
,利用点在曲线上,即可求得结论.
解答:解:设PQRS是与C外切,与C1内接的平行四边形,则PQRS是菱形,于是OP⊥OQ
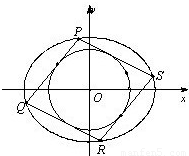
设P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),
则在直角△POQ中,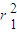 +
+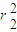 =
=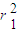
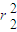 ,即
,即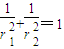
∵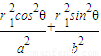 =1,即
=1,即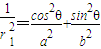
同理,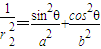 ,相加可得
,相加可得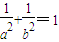
反之,若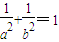 成立,则取P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),
成立,则取P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),
可得即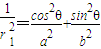 ,
,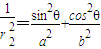 ,
,
∴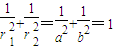
此时PQ与C2相切,即存在满足条件的平行四边形.
点评:本题考查圆与椭圆知识的综合,考查学生的分析解决问题能力,考查计算能力,综合性强.
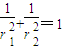 ,利用点在曲线上,即可求得结论.
,利用点在曲线上,即可求得结论.解答:解:设PQRS是与C外切,与C1内接的平行四边形,则PQRS是菱形,于是OP⊥OQ

设P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),
则在直角△POQ中,
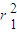 +
+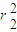 =
=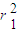
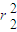 ,即
,即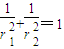
∵
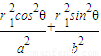 =1,即
=1,即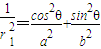
同理,
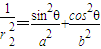 ,相加可得
,相加可得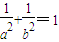
反之,若
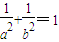 成立,则取P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),
成立,则取P(r1cosθ,r1sinθ),Q(r2cos(θ+90°),r2sin(θ+90°)),可得即
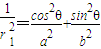 ,
,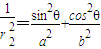 ,
,∴
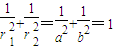
此时PQ与C2相切,即存在满足条件的平行四边形.
点评:本题考查圆与椭圆知识的综合,考查学生的分析解决问题能力,考查计算能力,综合性强.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知⊙C:x2+y2=1,点A(-2,0)和点B(2,a),从点A观察点B,要使视线不被⊙C挡住,则实数a的取值范围是( )
| A、(-∞,-2)∪(2,+∞) | ||||||||
B、(-∞,-
| ||||||||
C、(-∞,-
| ||||||||
D、(-
|
已知⊙C:x2+y2+Dx+Ey+F=0,则F=E=0且D<0是⊙C与y轴相切于原点的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |