题目内容
20.函数y=cos2(ωx)的最小正周期为$\frac{π}{2}$,则ω等于( )| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
分析 由条件利用半角公式化简函数的解析式,再利用函数y=Asin(ωx+φ)的周期为 $\frac{2π}{ω}$,求得ω的值.
解答 解:∵函数y=cos2(ωx)=$\frac{1+cos2ωx}{2}$ 的最小正周期为$\frac{2π}{2ω}$=$\frac{π}{2}$,则ω=2,
故选:B.
点评 本题主要考查半角公式的应用,利用了函数y=Asin(ωx+φ)的周期为 $\frac{2π}{ω}$,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.如图所示的是一个几何体的三视图,则它的表面积为( )
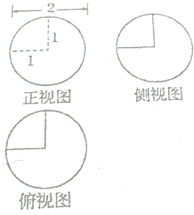

| A. | 4π | B. | $\frac{15π}{4}$ | C. | 5π | D. | $\frac{17π}{4}$ |
12.一质点由A点出发沿直线AB运动,先以加速度大小为a1的匀加速运动,接着做加速度为a2的匀减速直线运动,抵达B点时恰好静止,如果AB的总长度为S,试求质点走完AB全程所用时间t.(用多种方法求解)
9.已知集合A={y|y=-x2+5x-4,x∈R},则有( )
| A. | 1∈A且4∈A | B. | 1∈A但4∉A | C. | 1∉A但4∈A | D. | 1∉A且4∉A |