题目内容
下列函数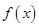 中,满足“对任意的
中,满足“对任意的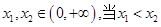 时,都有
时,都有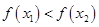 ”的是( )
”的是( )
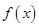 中,满足“对任意的
中,满足“对任意的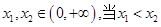 时,都有
时,都有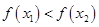 ”的是( )
”的是( )A.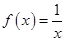 | B.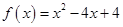 |
C.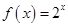 | D.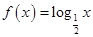 |
C
试题分析:对任意
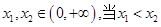 ,都有f(x1)<f(x2),即说明f(x)在
,都有f(x1)<f(x2),即说明f(x)在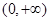 上单调递增,而
上单调递增,而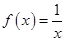 ,
,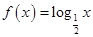 在区间
在区间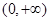 上均单调递减,
上均单调递减,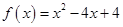
在 (-∞,2)是减函数,在(2,+∞)是增函数,只有函数
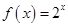 是单调递增函数,
是单调递增函数,故选C。
点评:简单题,熟练掌握常见函数的单调性,是解题的关键。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
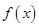 中,满足“对任意的
中,满足“对任意的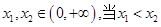 时,都有
时,都有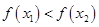 ”的是( )
”的是( )A.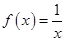 | B.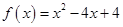 |
C.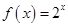 | D.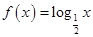 |
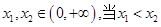 ,都有f(x1)<f(x2),即说明f(x)在
,都有f(x1)<f(x2),即说明f(x)在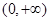 上单调递增,而
上单调递增,而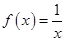 ,
,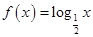 在区间
在区间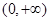 上均单调递减,
上均单调递减,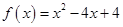
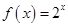 是单调递增函数,
是单调递增函数,
 阅读快车系列答案
阅读快车系列答案