题目内容
已知 为等差数列
为等差数列 的前
的前 项和,
项和, .
.
⑴求 ;
;
⑵求 ;
;
⑶求 .
.
(1)
 ;(2)
;(2)
 ;
;
(3)
 .
.
解析试题分析:先由通项公式与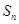 的关系式
的关系式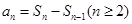 ,求出数列
,求出数列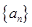 的通项公式
的通项公式 ,注意检验
,注意检验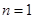 的情形是否成立,由此得出,当
的情形是否成立,由此得出,当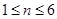 时,
时, ,当
,当 时,
时, .(1)
.(1)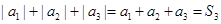 ,代入
,代入 即可计算;(2)
即可计算;(2)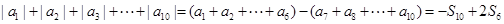 ,代入
,代入 即可解决;(3)需要对
即可解决;(3)需要对 进行分类,当
进行分类,当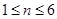 时,
时,
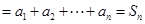 ,当
,当 时,
时,
 ,代入
,代入 ,问题得以解决.
,问题得以解决.
试题解析:
 ,
, 当
当 时,
时,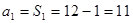 ,
,
当 时,
时, ,
,
当 时,
时, ,
,
 .
.
由 ,得
,得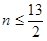 ,
, 当
当 时,
时, ;当
;当 时,
时, .
.
⑴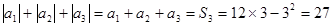 ;
;
⑵
 ;
;
⑶当 时,
时, ,
,
当 时,
时,
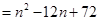
所以
 .
.
考点:1.等差数列的通项公式;2.等差数列的前 项和公式.
项和公式.

练习册系列答案
相关题目
 的前
的前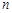 项和
项和 ,数列
,数列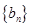 满足
满足 .
.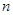 项和
项和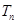 .
.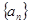 的前n项和为
的前n项和为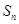 ,且
,且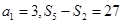 ,
,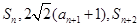 成等比数列,求正整数n的值.
成等比数列,求正整数n的值.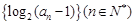 为等差数列,且
为等差数列,且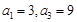 .
.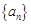 的通项公式;
的通项公式;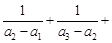
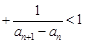 .
.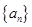 为等差数列,且
为等差数列,且 .
.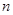 项和为
项和为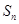 ,若
,若 成等比数列,求正整数
成等比数列,求正整数 的值.
的值. 为等差数列,其公差d不为0,
为等差数列,其公差d不为0, 和
和 的等差中项为11,且
的等差中项为11,且 ,令
,令 ,数列
,数列 的前n项和为
的前n项和为 .
. 及
及 成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.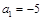 ,
,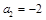 ,记
,记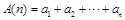 ,
,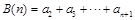 ,
,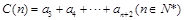 ,若对于任意
,若对于任意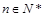 ,A(n),B(n),C(n)成等差数列.
,A(n),B(n),C(n)成等差数列.
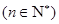 中,其前
中,其前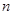 项和为
项和为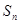 ,满足
,满足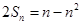 .
.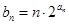 ,求数列
,求数列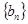 的前
的前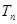 .
.