题目内容
在数列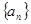
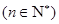 中,其前
中,其前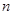 项和为
项和为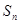 ,满足
,满足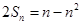 .
.
(1)求数列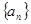 的通项公式;
的通项公式;
(2)设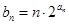 ,求数列
,求数列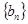 的前
的前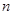 项和
项和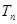 .
.
(1) 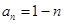 .(2)
.(2)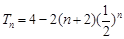 .
.
解析试题分析: (1)根据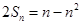 ,计算
,计算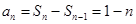
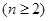
验证当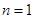 时,
时,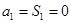 ,明确数列
,明确数列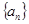 是
是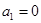 为首项、公差为
为首项、公差为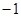 的等差数列即得所求.
的等差数列即得所求.
(2)由(1)知: 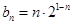 ,利用“错位相减法”求和.
,利用“错位相减法”求和.
试题解析: (1)由题设得: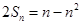 ,所以
,所以
所以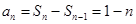
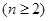 2分
2分
当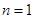 时,
时,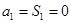 ,数列
,数列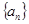 是
是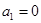 为首项、公差为
为首项、公差为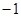 的等差数列
的等差数列
故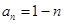 . 5分
. 5分
(2)由(1)知: 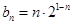
所以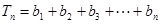
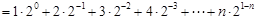
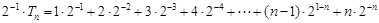 8分
8分
两式相减得: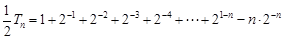
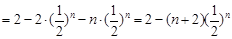 .
.
所以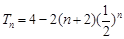 . 12分
. 12分
考点:等差数列的通项公式,“错位相减法”.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
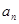 }中,
}中,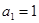 ,
,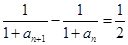
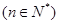 ,
,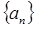 的通项公式
的通项公式 (
(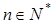 ),求数列
),求数列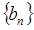 的前10项和
的前10项和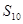 .
. 为等差数列
为等差数列 的前
的前 项和,
项和, .
. ;
;  ;
; .
. }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列. =
= ,求数列{
,求数列{ .
.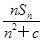 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数. 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.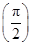 =0.
=0.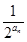 ),求数列{bn}的前n项和Sn.
),求数列{bn}的前n项和Sn.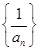 是等差数列并求数列{an}的通项公式;
是等差数列并求数列{an}的通项公式;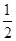 .
. 求a1+a2+a3+a4+…+a99+a100的值.
求a1+a2+a3+a4+…+a99+a100的值.