题目内容
已知数列{an},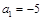 ,
,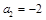 ,记
,记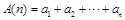 ,
,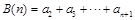 ,
,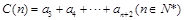 ,若对于任意
,若对于任意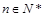 ,A(n),B(n),C(n)成等差数列.
,A(n),B(n),C(n)成等差数列.
(1)求数列{an}的通项公式;
(2)求数列{|an|}的前n项和.
(1)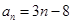 (2)
(2)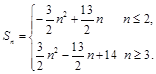
解析试题分析:(1)A(n),B(n),C(n)成等差数列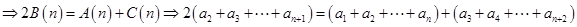
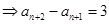 ,可知数列{an}是等差数列.
,可知数列{an}是等差数列.
(2)由第(1)的结论知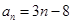 ,所以当
,所以当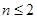 时
时  ;当
;当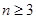 时,
时, 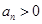
于是:当所以当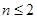 时
时  ,数列{|an|}成等差,首项为
,数列{|an|}成等差,首项为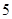 ,公差为
,公差为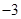 ,由等差数列求和公式求解;
,由等差数列求和公式求解;
或直接求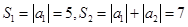
当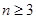 时,数列{|an|}从第三项起成等差数列,可由等差数列求和公式解决,或作如下变化:
时,数列{|an|}从第三项起成等差数列,可由等差数列求和公式解决,或作如下变化: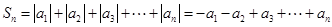
=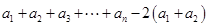 =
=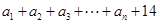 其余便可由等差数列求和公式直接求解.
其余便可由等差数列求和公式直接求解.
试题解析:
解:(1)根据题意A(n), B(n), C(n)成等差数列, ∴A(n)+ C(n)=2 B(n); 2分
整理得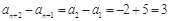 ,
,
∴数列{an}是首项为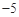 ,公差为3的等差数列. 4分
,公差为3的等差数列. 4分
∴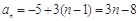 ;..........................6分
;..........................6分
(2)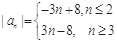 , 记数列
, 记数列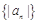 的前n项和为Sn.
的前n项和为Sn.
当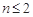 时,
时,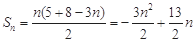 ;9分
;9分
当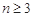 时,
时, ;.11分
;.11分
综上, . ..12分
. ..12分
考点:1、等差数列的通项公式与前 项和公式;2、等差中项的性质.
项和公式;2、等差中项的性质.

练习册系列答案
相关题目
 是正数组成的数列,其前
是正数组成的数列,其前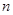 项和为
项和为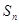 ,且对所有的正整数
,且对所有的正整数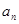 与2的等差中项等于
与2的等差中项等于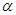 为锐角,且
为锐角,且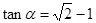 ,函数
,函数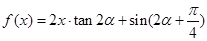 ,数列
,数列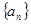 的首项
的首项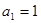 ,
, .
.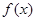 的表达式;(2)求数列
的表达式;(2)求数列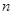 项和
项和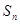 .
. 为等差数列
为等差数列 的前
的前 项和,
项和, .
. ;
;  ;
; .
.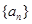 的前四项和
的前四项和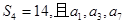 成等比.
成等比.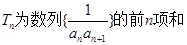 ,若
,若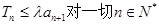 恒成立,求实数
恒成立,求实数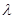 的最大值.
的最大值. }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列. =
= ,求数列{
,求数列{ .
.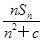 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数. 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.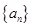 的首项为
的首项为 ,公差为
,公差为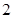 ,等比数列
,等比数列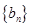 的首项为
的首项为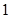 ,公比为
,公比为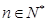 .
.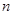 个正方形的边长为
个正方形的边长为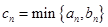 ,求前
,求前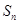 .
. 表示
表示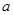 与
与 的最小值.)
的最小值.)