题目内容
已知数列 为等差数列,其公差d不为0,
为等差数列,其公差d不为0, 和
和 的等差中项为11,且
的等差中项为11,且 ,令
,令 ,数列
,数列 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)是否存在正整数m,n(1<m<n),使得 成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:本题主要考查等差数列、等比数列的定义、通项公式、性质以及裂项相消法求和等数学知识,考查学生的分析问题解决问题的能力和计算能力.第一问,先利用等差中项的概念将 和
和 的等差中项为11,转化为
的等差中项为11,转化为 ,与已知联立,利用等差数列的通项公式展开,解方程组得出基本量
,与已知联立,利用等差数列的通项公式展开,解方程组得出基本量 和
和 ,从而求出等差数列的通项公式,将
,从而求出等差数列的通项公式,将 代入到
代入到 中,利用裂项相消法求和;第二问,先假设存在m和n,利用已知看能不能求出m和n的值,利用第一问的结论
中,利用裂项相消法求和;第二问,先假设存在m和n,利用已知看能不能求出m和n的值,利用第一问的结论 ,得出
,得出 的值,由已知
的值,由已知 成等比数列,则
成等比数列,则 ,整理得到关于m,n的方程,通过解方程得出m和n的值.
,整理得到关于m,n的方程,通过解方程得出m和n的值.
试题解析:(Ⅰ)因为 为等差数列,公差为
为等差数列,公差为 ,则由题意得
,则由题意得
整理得
所以 3分
3分
由
所以 6分
6分
(Ⅱ)假设存在
由(Ⅰ)知, ,所以
,所以
若 成等比,则有
成等比,则有 8分
8分 ,(1)
,(1)
因为 ,所以
,所以 , 10分
, 10分
因为 ,当
,当 时,代入(1)式,得
时,代入(1)式,得 ;
;
综上,当 可以使
可以使 成等比数列。 12分
成等比数列。 12分
考点:1.等差数列的通项公式;2.等差中项;3.等比数列的定义;4.裂项相消法.

练习册系列答案
相关题目
 的等比数列
的等比数列 不是递减数列,其前n项和为
不是递减数列,其前n项和为 ,且
,且 成等差数列。
成等差数列。 ,求数列
,求数列 的最大项的值与最小项的值。
的最大项的值与最小项的值。 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列 的一个是等比数列的子列;
的一个是等比数列的子列; ,公比
,公比 且
且 ,则数列
,则数列 的公差为
的公差为 ,且
,且 .若设
.若设 是从
是从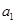 开始的前
开始的前 项数列的和,即
项数列的和,即 ,
, ,如此下去,其中数列
,如此下去,其中数列 是从第
是从第 开始到第
开始到第 )项为止的数列的和,即
)项为止的数列的和,即 .
. ,试找出一组满足条件的
,试找出一组满足条件的 ,使得:
,使得:  ;
; ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列 中的各数都为平方数;
中的各数都为平方数; .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列 ,使得
,使得 为等差数列
为等差数列 的前
的前 项和,
项和, .
. ;
;  ;
; .
. 的前n项和为Sn,已知
的前n项和为Sn,已知 ,且
,且 对一切
对一切 都成立.
都成立. }的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列.
}的前n项和为Sn,公差d≠0,且S3=9,a1,a3,a7成等比数列. =
= ,求数列{
,求数列{ .
. 求a1+a2+a3+a4+…+a99+a100的值.
求a1+a2+a3+a4+…+a99+a100的值.