题目内容
已知数列 的各项均满足
的各项均满足 ,
, ,
,

(1)求数列 的通项公式;
的通项公式;
(2)设数列 的通项公式是
的通项公式是 ,前
,前 项和为
项和为 ,求证:对于任意的正数
,求证:对于任意的正数 ,总有
,总有 .
.
(1) an=3n (2)见解析
解析试题分析:(1)由 ,可知数列
,可知数列 为等比数列,由
为等比数列,由 ,
, 易知首项为3,公比为3 ,可得通项公式an=3n.(2)将上题所求代入可知bn=
易知首项为3,公比为3 ,可得通项公式an=3n.(2)将上题所求代入可知bn= ,此种类型的数列用裂项法求前
,此种类型的数列用裂项法求前 项和为
项和为 =1-
=1- 由不等式易知
由不等式易知 .
.
试题解析:(1)解 由已知得 数列 是等比数列. 2分
是等比数列. 2分
因为a1=3, ∴an=3n. 5分
∴an=3n. 5分
(2)证明 ∵bn= =
= . 7分
. 7分
∴Tn=b1+b2++bn= +
+ ++
++ =1-
=1- <1. 12分
<1. 12分
考点:本题主要考查等比数列的定义,通项公式.裂项法求数列的通项公式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 中,已知
中,已知 ,
, ,
, .
.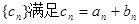 ,求
,求 的前
的前 项和
项和 .
. 中,
中, ,
, ,记
,记 为
为 项的和,
项的和, ,
, .
. 是否为等比数列,并求出
是否为等比数列,并求出 ;
;  N*,都有
N*,都有 .
. ,求证:数列
,求证:数列 为等比数列;
为等比数列; .
. 的前n项的和为
的前n项的和为 ,且
,且 ,
,
 是等比数列
是等比数列 与前n项的和
与前n项的和 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围. ,其前
,其前 项和
项和 满足
满足 且
且 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; 表示不超过实数
表示不超过实数 的最大整数,记
的最大整数,记 ,求
,求 .
. +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项. 满足前
满足前 项和
项和 .
. 的前
的前 .
.