题目内容
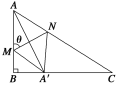
【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
【答案】见解析
【解析】解 (1)由∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a,
a,
所以∠BAC=![]() .
.
设MA=MA′=xa(0<x<1),则MB=a-xa,
所以在Rt△MBA′中,cos(π-2θ)=![]() =
=![]() ,
,
所以x=![]() .
.
由于△AMN为等边三角形,
所以绿地的面积
S=2×![]() ×
×![]() a×
a×![]() a×sin
a×sin![]() =
=![]() a2.
a2.
(2)因为在Rt△ABC中,∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a,
a,
所以∠BAC=![]() ,所以在△AMN中,∠ANM=
,所以在△AMN中,∠ANM=![]() -θ,
-θ,
由正弦定理得![]() =
=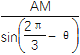 ,
,
设AM=ax(0<x<1),则A′M=ax,BM=a-ax,
所以在Rt△MBA′中,cos(π-2θ)=![]() =
=![]() ,
,
所以x=![]() ,即AM=
,即AM=![]() ,
,
所以AN= .
.
2sinθsin![]() =sin2θ+
=sin2θ+![]() sinθcosθ
sinθcosθ
=![]() +
+![]() sin2θ-
sin2θ-![]() cos2θ=
cos2θ=![]() +sin(2θ-
+sin(2θ-![]() ),
),
因为![]() <θ<
<θ<![]() ,所以
,所以![]() <2θ-
<2θ-![]() <
<![]() ,
,
所以当且仅当2θ-![]() =
=![]() ,即θ=
,即θ=![]() 时,AN的值最小,且AN=
时,AN的值最小,且AN=![]() a,此时绿地公共走道的长度MN=
a,此时绿地公共走道的长度MN=![]() a.
a.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.