Question

【题目】如图，已知正方体 的棱长为3，M，N分别是棱 、 上的点，且 .
（1）证明： 四点共面；
（2）求几何体 的体积.

Answer 1

【答案】
（1）解：证明：∵ ， ，又 ， ，
∴ ，且 ，
连接 ，则四边形 是平行四边形，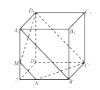

所以
在 中， ， ，
所以 ，所以
所以 ，所以 四点共面.
（2）解：因为平面 平面 ，
又 四点共面，所以平面 平面
延长 与 相交于点 ，因为
所以 ，即 ，解得 ，同理可得 ，所以点 与点 重合
所以 三线相交于一点，
所以几何体 是一个三棱台
所以 .
【解析】(1)由M,N分别为棱的中点,通过证明MN//A1B,得到四点共线.
(2)分析出几何体是一个三棱台,用体积公式求解.