题目内容
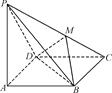
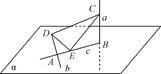
如图,三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是AC,AD上的动点,且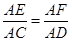 =λ(0<λ<1).
=λ(0<λ<1).
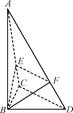
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD..
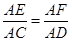 =λ(0<λ<1).
=λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD..
(1)见解析(2)λ=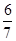
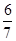
(1)证明:∵AB⊥平面BCD,∴AB⊥CD.
∵CD⊥BC,且AB∩BC=B,∴CD⊥平面ABC.
∵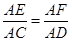 =λ(0<λ<1),
=λ(0<λ<1),
∴不论λ为何值,恒有EF∥CD.
∴EF⊥平面ABC,EF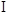 平面BEF.
平面BEF.
∴不论λ为何值恒有平面BEF⊥平面ABC.
(2)解:由(1)知,BE⊥EF,∵平面BEF⊥平面ACD,∴BE⊥平面ACD.∴BE⊥AC.
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=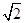 ,AB=
,AB=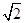 tan60°=
tan60°=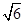 .
.
∴AC= =
= .
.
由AB2=AE·AC,得AE=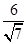 .∴λ=
.∴λ= =
=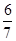 .
.
故当λ=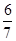 时,平面BEF⊥平面ACD
时,平面BEF⊥平面ACD
∵CD⊥BC,且AB∩BC=B,∴CD⊥平面ABC.
∵
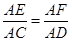 =λ(0<λ<1),
=λ(0<λ<1),∴不论λ为何值,恒有EF∥CD.
∴EF⊥平面ABC,EF
 平面BEF.
平面BEF.∴不论λ为何值恒有平面BEF⊥平面ABC.
(2)解:由(1)知,BE⊥EF,∵平面BEF⊥平面ACD,∴BE⊥平面ACD.∴BE⊥AC.
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=
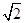 ,AB=
,AB=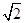 tan60°=
tan60°=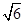 .
.∴AC=
 =
= .
.由AB2=AE·AC,得AE=
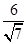 .∴λ=
.∴λ= =
=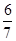 .
.故当λ=
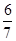 时,平面BEF⊥平面ACD
时,平面BEF⊥平面ACD
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

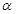 ,下列命题正确的是( )
,下列命题正确的是( ) 则
则
 则
则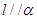
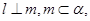 则
则
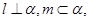 则
则