已知直线x-y-5=0与圆x2+y2-4x+6y-12=0相交于A.B两点.则弦AB的长为( )A．5B．8C．10D．12 题目和参考答案——青夏教育精英家教网—

题目内容

8．已知直线x-y-5=0与圆x²+y²-4x+6y-12=0相交于A、B两点，则弦AB的长为（　　）

A．

B．

C．

D．

分析圆的方程化为标准方程，直线x-y-5=0经过圆心（2，-3），即可求出弦AB的长．

解答解：圆x²+y²-4x+6y-12=0可化为（x-2）²+（y+3）²=25，圆心坐标为（2，-3），半径为5．
直线x-y-5=0经过圆心（2，-3），∴弦AB的长为10．
故选：C．

点评本题给出直线与圆相交，求截得弦的长度．着重考查了直线与圆的位置关系的知识，属于基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

7．已知全集U=R，集合A={x|lgx≤0]，B={x|2^x≤$\root{3}{2}$}，则A∪B=（-∞，1]．

16．已知f（x）=$\left\{\begin{array}{l}{{2}^{x}（x≤0）}\\{lo{g}_{2}x（x＞0）}\end{array}\right.$，若f（a）+f（1）=$\frac{1}{2}$，则a=-1或$\sqrt{2}$．

3．已知M₀是（x₀，y₀）是x²+y²=a²（a＞0）内一点，则判断l：x₀x+y₀y=a²与圆的位置关系．

13．在三棱锥P-ABC中，平面PAB⊥平面ABC，PA=PB，AC⊥BC，AB=4，PC=6，则三棱锥P-ABC的外接球O的表面积为（　　）

20．

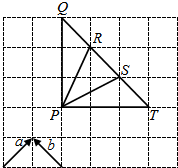如图所示，下列结论正确的是（　　）
①$\overrightarrow{PQ}$=$\frac{3}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$；②$\overrightarrow{PT}$=-$\frac{3}{2}$$\overrightarrow{a}$-$\frac{3}{2}$$\overrightarrow{b}$；③$\overrightarrow{PS}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$；④$\overrightarrow{PR}$=$\frac{3}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$．

17．求函数的值域，单调区间．
y=log${\;}_{\frac{1}{2}}$（x-1）-log${\;}_{\frac{1}{2}}$（x+3）

18．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x\\;x＞0}\\{{2}^{x}\\;x≤0}\end{array}\right.$，若f（1）+f（a）=2，则a的值为（　　）

试题分类