题目内容
.(本小题满分12分)
已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,f(x)>0,
当x∈(-∞,-2)∪(6 ,+∞)时,f(x)<0,
,+∞)时,f(x)<0,
(1)求f(x)的解析式.
(2)求f(x)在区间[1,10]上的最值。
解:(1)由题意得a<0,且x=-2,x=6是方程f(x)=0的两个根,由韦达定理得 得
得
∴. f(x)=-4x2+16x+48 …………………6分
(2)f(x)=-4x2+16x+48=-4(x-2)2+64
∴f max(x)=f(2)=64
f min (x)= f(10)=-192 …………………12分
f(10)=-192 …………………12分
解析

练习册系列答案
相关题目
(本小题满分12分) 为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第
为了预防流感,某段时间学校对教室用药熏消毒法进行消毒.设药物开始释放后第 小时教室内每立方米空气中的含药量为
小时教室内每立方米空气中的含药量为 毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
毫克.已知药物释放过程中,教室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为 (a为常数).函数图象如图所示.
(a为常数).函数图象如图所示.
根据图中提供的信息,解答下列问题:
(1)求从药物释放开始每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
|


 解析式并判断
解析式并判断 当
当 时都有
时都有 成立,求满足条件
成立,求满足条件 的实数m的取值范围。
的实数m的取值范围。 其中第二个函数和第三个函数中的
其中第二个函数和第三个函数中的 为同一个常数,且
为同一个常数,且 ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程 的三个根.
的三个根. ;
; 是函数
是函数 的两个极值点,求
的两个极值点,求 的取值范围.
的取值范围. (
( 为常数)的图象过点
为常数)的图象过点 ,
, 的奇偶性;
的奇偶性; 在区间
在区间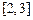 上
上 有意义,求实数
有意义,求实数 的取值范围;
的取值范围; 的方程
的方程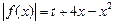
 (
( 为常数)的正根的个数.
为常数)的正根的个数. 有最大值
有最大值 , 且
, 且 , 其中实数
, 其中实数 是正整数.
是正整数. 的解析式;
的解析式; , 证明
, 证明 (
( 是正整数).
是正整数). 横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km). 在其定义域上满足
在其定义域上满足 .
. 的图象是否是中心对称图形?若是,请指出其对称中心(不证明);
的图象是否是中心对称图形?若是,请指出其对称中心(不证明); 时,求x的取值范围;
时,求x的取值范围; ,数列
,数列 满足
满足 ,那么:
,那么: ,正整数N满足
,正整数N满足 时,对所有适合上述条件的数列
时,对所有适合上述条件的数列 ,
,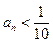 恒成立,求最小的N;
恒成立,求最小的N; ,求证:
,求证: .
.