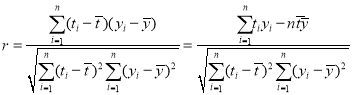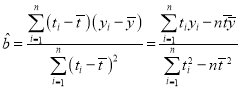题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的最大值;
的最大值;
(2)若对![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用导数分析函数![]() 的单调性,进而可求得函数
的单调性,进而可求得函数![]() 的最大值;
的最大值;
(2)由题意可知![]() ,对函数
,对函数![]() 求导,对实数
求导,对实数![]() 的取值进行分类讨论,利用导数分析函数
的取值进行分类讨论,利用导数分析函数![]() 在区间
在区间![]() 上的单调性,结合
上的单调性,结合![]() 可得出关于实数
可得出关于实数![]() 的不等式,进而可求得实数
的不等式,进而可求得实数![]() 的取值范围.
的取值范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
所以,函数![]() 在
在![]() 处取得极大值,亦即最大值,即
处取得极大值,亦即最大值,即![]() ;
;
(2)由题意可知![]() ,即
,即![]() .
.
![]() ,则
,则![]() ,所以,函数
,所以,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,即
,即![]() .
.
①当![]() 时,即当
时,即当![]() 时,
时,![]() 对任意的
对任意的![]() 恒成立,
恒成立,
此时,函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() ,
,
![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
②当![]() 时,即当
时,即当![]() 时,
时,![]() 对任意的
对任意的![]() 恒成立,
恒成立,
此时,函数![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,
![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
③当![]() 时,即当
时,即当![]() 时,则存在
时,则存在![]() ,使得
,使得![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

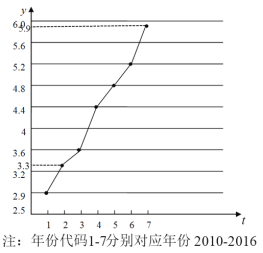
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
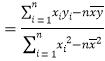 ,
,![]()
【题目】共享单车的投放,方便了市民短途出行,被誉为中国“新四大发明”之一.某市为研究单车用户与年龄的相关程度,随机调查了100位成人市民,统计数据如下:
不小于40岁 | 小于40岁 | 合计 | |
单车用户 | 12 | y | m |
非单车用户 | x | 32 | 70 |
合计 | n | 50 | 100 |
(1)求出列联表中字母x、y、m、n的值;
(2)①从此样本中,对单车用户按年龄采取分层抽样的方法抽出5人进行深入调研,其中不小于40岁的人应抽多少人?
②从独立性检验角度分析,能否有![]() 以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
以上的把握认为该市成人市民是否为单车用户与年龄是否小于40岁有关.
下面临界值表供参考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6635 | 7.879 | 10.828 |