题目内容
11.某个停车场有一排共12个车位,从入口开始依次编号是1号停车位、2号停车位、…、12号停车位.早上来了8辆车,随机地停在了其中8个车位.(1)这时有一辆体型较大的工程车到达停车场,它需要占据两个相邻的车位,求工程车能停进车位的概率;
(2)求没有三辆车相邻的概率;
(3)如果有4辆车离开之后,又有一辆车开进来,停在离入口最近的空车位,记这个车位的编号是η,求η的期望.
分析 (1)先求出基本事件总数n=${C}_{12}^{8}$,工程车能停进车位,要求有两个空车位相邻,求出包含的基本事件个数m1=${C}_{12}^{8}-{C}_{9}^{4}$,由此能求出工程车能停进车位的概率.
(2)“没有3辆车相邻”的可能性包括:①车车空车车空车车空车车,剩下一个车位可能与空车位相邻也可能在最前面或在最后面,有5种排法;②先排好四个空车位,有${C}_{4}^{4}$种排法,空空空空,四个空位间有五个间隔,从中选两个间隔各放一辆车,有${C}_{5}^{2}$种放法,另外三个间隔各放两辆车,有1种放法,由分步计数原理得有${C}_{4}^{4}{×C}_{5}^{2}×1$=10种排法,由此能求出没有三辆车相邻的概率.
(3)由已知得η的可能取值为1,2,3,4,5,分别求出相应的概率,由此能求出η的期望.
解答 解:(1)某个停车场有一排共12个车位,8辆车随机地停在了其中8个车位,
基本事件总数n=${C}_{12}^{8}$,
工程车能停进车位,要求有两个空车位相邻,包含的基本事件个数:
m1=${C}_{12}^{8}-{C}_{9}^{4}$,
∴工程车能停进车位的概率:p1=$\frac{{m}_{1}}{n}$=$\frac{{C}_{12}^{8}-{C}_{9}^{4}}{{C}_{12}^{8}}$=$\frac{41}{55}$.
(2)“没有3辆车相邻”的可能性包括:
①车车空车车空车车空车车,剩下一个车位可能与空车位相邻也可能在最前面或在最后面,有5种排法,
②先排好四个空车位,有${C}_{4}^{4}$种排法,空空空空,四个空位间有五个间隔,
从中选两个间隔各放一辆车,有${C}_{5}^{2}$种放法,另外三个间隔各放两辆车,有1种放法,
由分步计数原理得有${C}_{4}^{4}{×C}_{5}^{2}×1$=10种排法,
∴没有三辆车相邻的概率${p}_{2}=\frac{5+10}{{C}_{12}^{4}}$=$\frac{1}{33}$.
(3)由已知得η的可能取值为1,2,3,4,5,
P(η=1)=$\frac{{C}_{11}^{4}}{{C}_{12}^{4}}$=$\frac{2}{3}$,
P(η=2)=$\frac{{C}_{10}^{3}}{{C}_{12}^{4}}$=$\frac{8}{33}$,
P(η=3)=$\frac{{C}_{9}^{2}}{{C}_{12}^{4}}$=$\frac{4}{55}$,
P(η=4)=$\frac{{C}_{8}^{1}}{{C}_{12}^{4}}$=$\frac{8}{495}$,
P(η=5)=$\frac{1}{{C}_{12}^{4}}$=$\frac{1}{495}$.
∴Eη=1×$\frac{2}{3}$+2×$\frac{8}{33}$+3×$\frac{4}{55}$+4×$\frac{8}{495}$+5×$\frac{1}{495}$=$\frac{13}{9}$.
点评 本题考查概率的求法,考查离散型随机变量的数学期望的求法,是中档题,解题时要注意分类讨论思想、分步计数原理和排列组合知识的合理运用.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | $\frac{7}{2}\sqrt{2}$ | B. | $14\sqrt{2}$ | C. | $7\sqrt{2}$ | D. | $\frac{7}{3}\sqrt{6}$ |
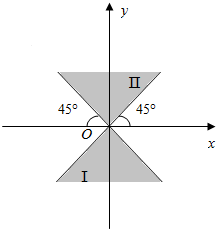 已知角α的终边在图中阴影表示的范围内(不包括边界),那么角α的集合是{α|k•180°+45°<α<k•180°+135°,k∈Z}.
已知角α的终边在图中阴影表示的范围内(不包括边界),那么角α的集合是{α|k•180°+45°<α<k•180°+135°,k∈Z}.