题目内容
2.已知函数f(x)=4x3-3x2cosθ+$\frac{3}{16}$cosθ其中x∈R,θ为参数,且0≤θ≤2π.(1)当cosθ=0时,判断函数f(x)是否有极值;
(2)要使函数f(x)的极小值大于零,求参数θ的取值范围.
分析 (1)通过cosθ=0,化简函数的解析式,利用导函数的单调性判断函数f(x)是否有极值;
(2)通过f′(x)=0,求出极值点x1=0,x2=$\frac{cosθ}{2}$.判断函数的单调性,然后求解使函数f(x)在R上的极小值大于零,参数θ的取值范围.
解答 解:(1)当cosθ=0时,f(x)=4x3,f′(x)=12x2≥0,
则f(x)在(-∞,+∞)内是增函数,故无极值.
(2)f′(x)=12x2-6xcosθ,令f′(x)=0,可得x1=0,x2=$\frac{cosθ}{2}$.
当cosθ>0时,容易判断f(x)在(-∞,0],$[\frac{cosθ}{2},+∞)$上是增函数,
在$[0,\frac{cosθ}{2}]$上是减函数,
故f(x)在x=$\frac{cosθ}{2}$处取得极小值:f($\frac{cosθ}{2}$)=$-\frac{1}{4}$${cos}^{3}θ+\frac{3}{16}cosθ$.
由$f(\frac{cosθ}{2})>0$,即$-\frac{1}{4}{cos}^{3}θ+\frac{3}{16}cosθ$>0,可得$0<cosθ<\frac{\sqrt{3}}{2}$,由于0≤θ≤2π,
$\frac{π}{6}<θ<\frac{π}{2}$或故$\frac{3π}{2}<θ<\frac{11π}{6}$.
同理,可知当cosθ<0时,f(x)在x=0处取极小值f(0)=$\frac{3}{16}$cosθ>0,
即cosθ>0,与cosθ<0矛盾,
所以当cosθ<0时,f(x)的极小值不会大于零.
综上,要使函数f(x)在R上的极小值大于零,参数θ的取值范围为$(\frac{π}{6},\frac{π}{2})∪(\frac{3π}{2},\frac{11π}{6})$.
点评 本题考查函数的对数的综合应用,函数的极值以及函数的单调性的判断与应用,考查计算能力.

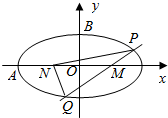 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.