题目内容
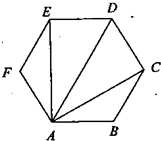在正六边形ABCDEF中（如图），下列说法错误的是（ ）分析：由题意，在正六边形ABCDEF中，根据所给的图象及正六边形的几何特征、向量的运算性质对四个选项进行验证，即可找出符合条件的选项
解答：解：由图，由于正六边形ABCDEF中
对于A选项，由于
+
=
+
=
=2
，故A选项中的等式正确；
对于B选项，由于
+
=
，故2
+2
=
，B选项中的等式正确；
对于C选项，由于
•
-
•
=
•(
)=
•
0故
•
=
•
不成立
对于D选项，由图知，
=-2
，所以(
•
)
=(-2
•
)
=-2
(
•
)=
(
•
)，即有(
•
)
=
(
•
)
综上知，C中说法是错误的，
故选C
对于A选项，由于
| AC |
| AF |
| AC |
| CD |
| AD |
| BC |
对于B选项，由于
| AB |
| AF |
| 1 |
| 2 |
| AD |
| AB |
| AF |
| AD |
对于C选项，由于
| AC |
| AD |
| AD |
| AB |
| AD |
| AC- |
| AB |
| AD |
| BC≠ |
| AC |
| AD |
| AD |
| AB |
对于D选项，由图知，
| AD |
| EF |
| AD |
| AF |
| EF |
| EF |
| AF |
| EF |
| EF |
| AF |
| EF |
| AD |
| AF |
| EF |
| AD |
| AF |
| EF |
| AD |
| AF |
| EF |
综上知，C中说法是错误的，
故选C
点评：本题考查向量数量积的运算，向量的加法，向量的共线及正六边形的几何特征，解题的关键是熟练掌握向量的运算及熟练掌握正六边形的几何特征，本题考查了依据图形进行判断推理的能力，考查了数形结合的思想，是向量中的基础题型
练习册系列答案
相关题目
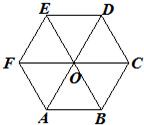O是正六边形ABCDE的中心，且
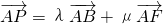（λ，μ∈R）则λ+μ的取值范围
（λ，μ∈R）则λ+μ的取值范围（ ）