题目内容
如图,在正六边形ABCDE中,点P是△CDE内(包括边界)的一个动点,设 (λ,μ∈R)则λ+μ的取值范围( )
(λ,μ∈R)则λ+μ的取值范围( )A.[1,2]
B.[2,3]
C.[2,4]
D.[3,4]
【答案】分析:通过建立坐标系,写出点的坐标及直线方程,设动点P的坐标写出动点P的可行域;写出向量的坐标,据已知条件中的向量等式得到λ,μ与x,y的关系代入点P的可行域得λ,μ的可行域,利用线性规划求出λ+μ的取值范围
解答: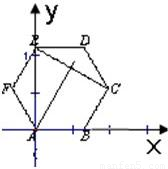 解:建立如图坐标系,设AB=2,则A(0,0),B(2,0),
解:建立如图坐标系,设AB=2,则A(0,0),B(2,0),
C(3,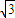 ),D(2,2
),D(2,2 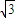 ),E(0,2
),E(0,2 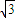 ),F(-1,
),F(-1,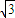 )
)
则EC的方程:x+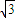 y-6=0;CD的方程:
y-6=0;CD的方程: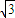 x+y-4
x+y-4 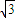 =0;
=0;
因P是△CDE内(包括边界)的动点,则可行域为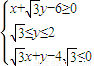
又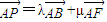 ,
,
则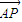 =(x,y),
=(x,y),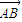 =(2,0),
=(2,0),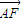 =(-1,
=(-1,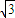 ),
),
所以(x,y)=λ(2,0)+μ(-1,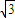 )
)
得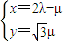 ⇒
⇒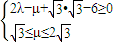 ⇒
⇒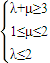 ⇒3≤λ+μ≤4.
⇒3≤λ+μ≤4.
则λ+μ的取值范围为[3,4].
故选D.
点评:本题考查向量在几何中的应用,解答的关键是通过建立直角坐标系将问题转化为线性规划问题,通过线性规划求出范围.
解答:
 解:建立如图坐标系,设AB=2,则A(0,0),B(2,0),
解:建立如图坐标系,设AB=2,则A(0,0),B(2,0),C(3,
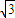 ),D(2,2
),D(2,2 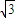 ),E(0,2
),E(0,2 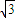 ),F(-1,
),F(-1,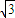 )
)则EC的方程:x+
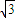 y-6=0;CD的方程:
y-6=0;CD的方程: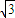 x+y-4
x+y-4 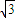 =0;
=0;因P是△CDE内(包括边界)的动点,则可行域为
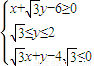
又
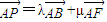 ,
,则
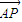 =(x,y),
=(x,y),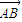 =(2,0),
=(2,0),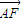 =(-1,
=(-1,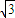 ),
),所以(x,y)=λ(2,0)+μ(-1,
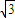 )
)得
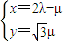 ⇒
⇒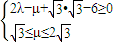 ⇒
⇒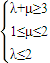 ⇒3≤λ+μ≤4.
⇒3≤λ+μ≤4.则λ+μ的取值范围为[3,4].
故选D.
点评:本题考查向量在几何中的应用,解答的关键是通过建立直角坐标系将问题转化为线性规划问题,通过线性规划求出范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
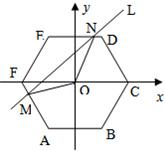 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
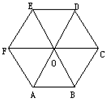 如图,在正六边形ABCDEF中,点O为其中心,则下列判断错误的是( )
如图,在正六边形ABCDEF中,点O为其中心,则下列判断错误的是( )