题目内容
（2009•台州一模）已知命题p：?x∈R，x2+
≤2，命题q是命题p的否定，则命题p、q、p∧q、p∨q中是真命题的是
| 1 | x2 |
p、p∨q
p、p∨q
．分析：先判断命题p的真假，然后根据复合命题与命题p，q的关键进行判断．
解答：解：因为x2+
≥2，当且仅当x=±1时取等号，所以当x=±1时，x2+
=2．
所以命题p为真命题，所以￢p为假命题，即q为假命题．
所以p∨q为真命题，p∧q为假命题．即命题p、q、p∧q、p∨q中是真命题的是p、p∨q．
故答案为：p、p∨q
| 1 |
| x2 |
| 1 |
| x2 |
所以命题p为真命题，所以￢p为假命题，即q为假命题．
所以p∨q为真命题，p∧q为假命题．即命题p、q、p∧q、p∨q中是真命题的是p、p∨q．
故答案为：p、p∨q
点评：本题考查特称命题的真假判断，以及基本不等式的应用，复合命题的真假判断．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
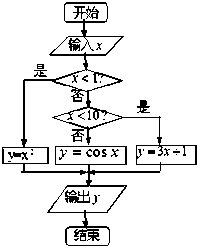（2009•台州一模）根据右边程序框图，若输出y的值是4，则输入的实数x=