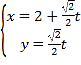Question

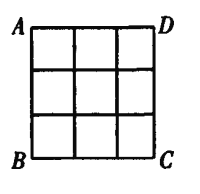
【题目】将随机地填入图正方形ABCD的九个格子中，每格填一数，则其每列三数自上而下、每行三数自左至右顺次成等差数列的概率P=____________.

Answer 1

【答案】

【解析】

设三行填数的和依次为.则也成等差；而 ，故.

设第二行三数依次为a、b、c(如图).

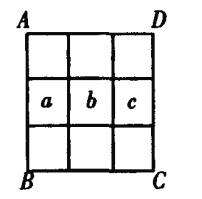
由a、b、c成等差数列,有a+b+c=15,得b=5.

于是，a+c=10.

{a,c}的取值只有{1,9}、{2,8}、{3,7}、{4,6}四种情形.

但a、c作为所在列的等差中项，不能取1和9.据对称性，1和9也不能在中间列，故只能在正方形的角方格上，且既不同行，也不同列(否则中项为5)，即1和9只能在正方形的对角方格上.

同理，{3,7}也不能被{a,c}取到.故3、7必在正方形的另一对角方格上.

于是，填法只有图的模式：它的各种情形，可看成将表格固定，然后将字母A放置于四角之一，再使正方形ABCD成顺时针或逆时针方向，共得8种情形(也可使正方形ABCD位置固定，而将数表旋转和翻折).

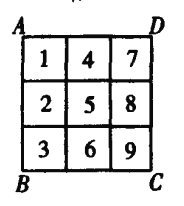
所以，.