题目内容
10.设函数f(x)=x|x-a|-x(x∈R).(1)试讨论f(x)的奇偶性;
(2)存在实数a对任意的x∈[0,t],不等式-4≤f(x)≤6恒成立,求实数t的最大值及此时a的值.
分析 (1)根据函数奇偶性的定义,讨论a=0和a≠0即可;
(2)利用参数分离法,将不等式恒成立进行转化为求函数的最值问题进行求解即可.
解答 解:(1)当a=0时,f(0)=0,f(x)=x|x|-x为奇函数,
当a≠0时,f(-a)+f(a)=-2a|a|≠0,则f(x)不是奇函数,
若f(x)是偶函数,则f(-x)=f(x),
即f(-x)-f(x)=x(2-|x+a|-|x-a|)=0恒成立,
∵2-|x+a|-|x-a|=0不恒成立,∴f(x)不是偶函数,
综上当a=0时,函数f(x)为奇函数,
当a≠0,f(x)为非奇非偶函数;
(2)当x=0时,f(0)=0,-4≤f(x)≤6恒成立,
当x∈[0,t],不等式-4≤f(x)≤6恒成立?-$\frac{4}{x}$+1≤|a-x|≤$\frac{6}{x}$+1
①当0<x<4时,?-$\frac{4}{x}$+1≤|a-x|恒成立,
|a-x|≤$\frac{6}{x}$+1?x-$\frac{6}{x}$-1≤a≤x+$\frac{6}{x}$+1恒成立,
②当t≥x≥4时,-$\frac{4}{x}$+1≤|a-x|≤$\frac{6}{x}$+1?$\left\{\begin{array}{l}{x-\frac{6}{x}-1≤a≤x+\frac{6}{x}+1}\\{a≤x+\frac{4}{x}-1或a≥x-\frac{4}{x}+1}\end{array}\right.$
?x-$\frac{4}{x}$+1≤a≤x+$\frac{6}{x}$+1或x-$\frac{6}{x}$-1≤a≤x+$\frac{4}{x}$-1恒成立,
∵4≤x≤t时,由x-$\frac{4}{x}$+1≤a≤x+$\frac{6}{x}$+1恒成立得,t-$\frac{4}{t}+1$≤2$\sqrt{6}$+1?t≤$\sqrt{6}+\sqrt{10}$,
由x-$\frac{6}{x}$-1≤a≤x+$\frac{4}{x}$-1恒成立,得t-$\frac{6}{t}-1≤4$⇒t≤6,
∵$\sqrt{6}+\sqrt{10}$<6,
∴t的最大值为6,此时6-$\frac{6}{6}$-1≤a≤4,解得a=4.
点评 本题主要考查函数奇偶性的判断,以及不等式恒成立问题,利用参数分离法将不等式进行转化是解决本题的关键.综合性较强,难度较大,注意要利用分类讨论的数学思想.

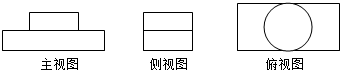
| A. |  | B. | 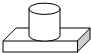 | C. | 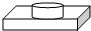 | D. | 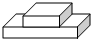 |
| A. | x${\;}^{-\frac{1}{3}}$ | B. | x${\;}^{\frac{2}{5}}$ | C. | x${\;}^{\frac{4}{15}}$ | D. | x${\;}^{-\frac{4}{15}}$ |
| A. | 3t | B. | $\frac{3}{2}$t | C. | t | D. | $\frac{t}{2}$ |
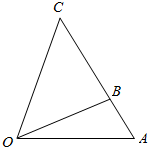 在2014年亚洲移动通信博览会上,中国移动表示投资将超过2400亿元,根据规划,某地移动公司需要在如图所示的三角形地带OAC区域内建造甲、乙两个基站,甲站建立在区域BOC内,乙站建立区域AOB内,分界线OB固定,且OB=(1+$\sqrt{3}$)km,边界线AC始终过点B,∠AOC=75°,∠AOB=30°,设OA=x(3≤x≤6)km,OC=ykm
在2014年亚洲移动通信博览会上,中国移动表示投资将超过2400亿元,根据规划,某地移动公司需要在如图所示的三角形地带OAC区域内建造甲、乙两个基站,甲站建立在区域BOC内,乙站建立区域AOB内,分界线OB固定,且OB=(1+$\sqrt{3}$)km,边界线AC始终过点B,∠AOC=75°,∠AOB=30°,设OA=x(3≤x≤6)km,OC=ykm