题目内容
给出以下四个命题:
① 若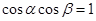 ,则
,则 ;
;
② 已知直线 与函数
与函数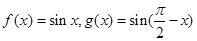 的图像分别交于点
的图像分别交于点 ,则
,则 的最大值为
的最大值为 ;
;
③ 若数列 为单调递增数列,则
为单调递增数列,则 取值范围是
取值范围是 ;
;
④ 已知数列 的通项
的通项 ,前
,前 项和为
项和为 ,则使
,则使 的
的 的最小值为12.
的最小值为12.
其中正确命题的序号为 .
①②
解析试题分析:因为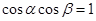 ,由余弦函数的值域知,
,由余弦函数的值域知,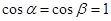 或
或 ,即
,即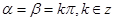 ,所以
,所以 ,①正确;
,①正确;
因为直线 与函数
与函数 的图像分别交于点
的图像分别交于点 ,
,  =|sinx-cosx|=
=|sinx-cosx|=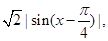 其最大值为
其最大值为 ,②正确;
,②正确;
借助于二次函数知识,图象的对称轴为n=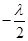 ,
,  为单调递增数列,
为单调递增数列,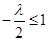 即可,即
即可,即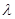
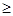 2,③不正确;
2,③不正确;
因为 ,所以
,所以 是递减数列,且前5项小于0,从第6项起各项均大于0.结合
是递减数列,且前5项小于0,从第6项起各项均大于0.结合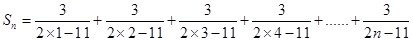 尝试知
尝试知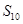 >0. ④不正确才,综上知,①②正确。
>0. ④不正确才,综上知,①②正确。
考点:本题主要考查三角恒等变换,三角函数图象和性质,数列的通项公式及前n项和。
点评:小综合题,这种类型的题目,在高考题中常常出现,扩大了知识考查的覆盖面,一般难度不大,主要运用数学的基础知识求解。

练习册系列答案
相关题目
 x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.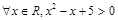 的否定是_________________.
的否定是_________________.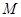 到两定点
到两定点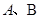 的距离之比为常数
的距离之比为常数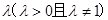 ,则动点
,则动点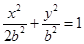 的离心率是
的离心率是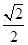 ;③双曲线
;③双曲线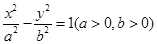 的焦点到渐近线的距离是b;④已知抛物线
的焦点到渐近线的距离是b;④已知抛物线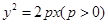 上两点
上两点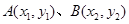 ,且OA⊥OB (O是坐标原点),则
,且OA⊥OB (O是坐标原点),则 .所有正确命题的序号是_______________.
.所有正确命题的序号是_______________. 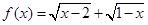 有意义; (2)函数是其定义域到值域的映射;
有意义; (2)函数是其定义域到值域的映射;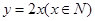 的图象是一直线;(4)函数
的图象是一直线;(4)函数 的图象是抛物线,
的图象是抛物线,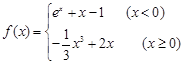 ,给出如下四个命题:
,给出如下四个命题: 在
在 上是减函数;②
上是减函数;② 有两个零点;④
有两个零点;④ 在R上恒成立.
在R上恒成立. ,则
,则 互为倒数”的逆命题;
互为倒数”的逆命题; ,则方程
,则方程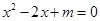 有实根”的逆否命题;
有实根”的逆否命题; ,则
,则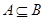 ”的逆否命题.
”的逆否命题.  ,给出下列命题:
,给出下列命题: 有最小值;
有最小值; 时,
时, ;
; 时,
时, 上有单调性;
上有单调性; .
.