题目内容
设0<a<1,0<b<1,则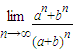 = .
= .
【答案】分析:利用二项展开式可得,(a+b)n=Cnan+cn1an-1b+…+cnnbn,代入可求极限
解答:解答:由于(a+b)n=Cnan+cn1an-1b+…+cnnbn
则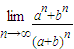 =
=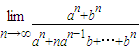 =
=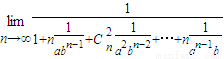 =0
=0
故答案为:0
点评:本题主要考查了二项展开式的应用,数列极限的求解,属于公式的综合应用,解题的关键是熟练掌握公式并能灵活利用.
解答:解答:由于(a+b)n=Cnan+cn1an-1b+…+cnnbn
则
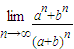 =
=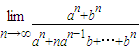 =
=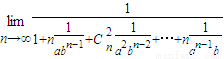 =0
=0故答案为:0
点评:本题主要考查了二项展开式的应用,数列极限的求解,属于公式的综合应用,解题的关键是熟练掌握公式并能灵活利用.

练习册系列答案
相关题目
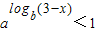 的解集是( )
的解集是( )