题目内容
设0＜a＜1，0＜b＜1且a≠b，则下列数中①a2+b2；②2ab；③2
；④
+
；⑤a+b．最大的数是
| ab |
| a |
| b |
④
④
；最小的数是②
②
．分析：利用已知和基本不等式即可得出．
解答：解：∵0＜a＜1，0＜b＜1且a≠b，∴a2＜a＜
，b2＜b＜
．
∴
+
＞a+b＞a2+b2＞2ab．
又a+b＞2
＞2ab．
∴a2+b2最大，2ab最小．
故答案分别为④，②．
| a |
| b |
∴
| a |
| b |
又a+b＞2
| ab |
∴a2+b2最大，2ab最小．
故答案分别为④，②．
点评：熟练掌握不等式的基本性质和基本不等式的性质是解题的关键．
练习册系列答案
相关题目
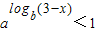的解集是（ ）
= ．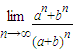