题目内容
(本小题满分12分)已知向量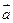 =(sin(
=(sin(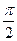 +x),
+x),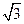 cosx),
cosx),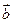 =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)= 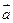 ·
·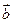 .
.
⑴求f(x)的最小正周期和单调增区间;
⑵如果三角形ABC中,满足f(A)=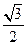 ,求角A的值.
,求角A的值.
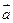 =(sin(
=(sin(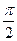 +x),
+x),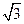 cosx),
cosx),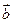 =(sinx,cosx), f(x)=
=(sinx,cosx), f(x)= 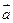 ·
·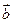 .
.⑴求f(x)的最小正周期和单调增区间;
⑵如果三角形ABC中,满足f(A)=
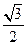 ,求角A的值.
,求角A的值.(Ⅰ) [kπ-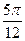 ,kπ+
,kπ+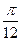 ],k∈Z. (Ⅱ) A=
],k∈Z. (Ⅱ) A=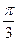 或
或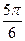
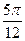 ,kπ+
,kπ+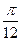 ],k∈Z. (Ⅱ) A=
],k∈Z. (Ⅱ) A=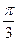 或
或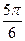
⑴f(x)= sinxcosx+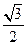 +
+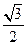 cos2x= sin(2x+
cos2x= sin(2x+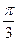 )+
)+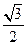 ………3分
………3分
T=π,2 kπ-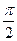 ≤2x+
≤2x+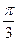 ≤2 kπ+
≤2 kπ+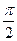 ,k∈Z,
,k∈Z,
最小正周期为π,单调增区间[kπ-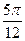 ,kπ+
,kπ+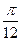 ],k∈Z.……………………6分
],k∈Z.……………………6分
⑵由sin(2A+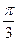 )=0,
)=0,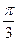 <2A+
<2A+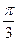 <
<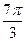 ,……………9分
,……………9分
∴2A+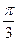 =π或2π,∴A=
=π或2π,∴A=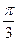 或
或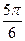 ……………………12分
……………………12分
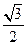 +
+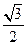 cos2x= sin(2x+
cos2x= sin(2x+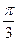 )+
)+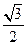 ………3分
………3分T=π,2 kπ-
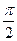 ≤2x+
≤2x+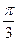 ≤2 kπ+
≤2 kπ+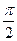 ,k∈Z,
,k∈Z,最小正周期为π,单调增区间[kπ-
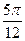 ,kπ+
,kπ+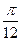 ],k∈Z.……………………6分
],k∈Z.……………………6分⑵由sin(2A+
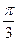 )=0,
)=0,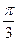 <2A+
<2A+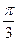 <
<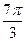 ,……………9分
,……………9分∴2A+
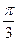 =π或2π,∴A=
=π或2π,∴A=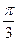 或
或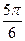 ……………………12分
……………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为 ,
, ,
,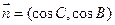 ,且
,且
 .(I)求
.(I)求 ;(
;( II)若
II)若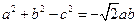 ,且
,且 ,求
,求 .
. |a-kb| (k>0).
|a-kb| (k>0).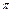 ,b=
,b= ,求a·b的最大值及相应的x值.
,求a·b的最大值及相应的x值.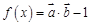 ,其中向量
,其中向量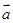 =(
=(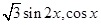 ),
),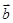 =(1,
=(1,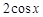 )(
)(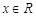 )(1)求
)(1)求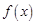 的最小正周期;(2)在△ABC中,角A、B、C的对边分别为
的最小正周期;(2)在△ABC中,角A、B、C的对边分别为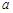 、
、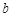 、
、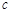 ,
,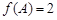 ,
,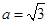 ,
,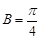 ,求边长b的值.
,求边长b的值. ,
, .
.  ,求函数
,求函数 关于
关于 的解析式;
的解析式; 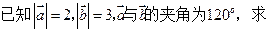
 ;
;
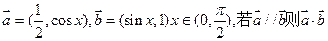 =" " ( )
=" " ( )


 与
与 的夹角为
的夹角为 ,且
,且 ,那么
,那么 的值为 。
的值为 。