题目内容
10.已知f(x)=log2(1+ax),g(x)=log2(1-x)(1)若f(x)-g(x)是奇函数,求实数a的值;
(2)当a=2时,f(x)+g(x)有最大值和最小值吗?,若有,求出其最大值和最小值;若没有,请说明理由.
分析 (1)得出F(x)=log2$\frac{1+ax}{1-x}$,运用奇偶函数的定义证明.
(2)得出函数关系式G(x)=f(x)+g(x)=log2(-2x2+x+1),结合不等式0<-2x2+x+1≤$\frac{9}{8}$.根据复合函数的单调性求解即可.
解答 解:∵f(x)=log2(1+ax),g(x)=log2(1-x)
∴F(x)=f(x)-g(x)=log2$\frac{1+ax}{1-x}$,
(1)∵f(x)-g(x)是奇函数,
∴F(-x)=-F(x),
即log2$\frac{1-ax}{1+x}$=-log2$\frac{1+ax}{1-x}$.
$\frac{1-ax}{1+x}$=$\frac{1-x}{1+ax}$,a2=1,a=-1(舍去)
a=1.
∴实数a的值为:1
(2)a=2,
G(x)=f(x)+g(x)=log2(-2x2+x+1)(-$\frac{1}{2}$<x<1)
∵0<-2x2+x+1=-2(x-$\frac{1}{4}$)2+$\frac{9}{8}$≤$\frac{9}{8}$.
当x=$\frac{1}{4}$∈(-$\frac{1}{2}$,1)时,等号成立.
∴利用对数函数对单调性得出:G(x)≤log2$\frac{9}{8}$.
∴f(x)+g(x)有最大值log2$\frac{9}{8}$,无最小值.
点评 本题综合考察了函数的性质,复合函数的性质运用,不等式的应用,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
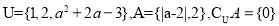 ,则a的值为
,则a的值为