题目内容
1.若一个直角三角形的三边长a<b<c,b2=ac,则该三角形的最小角的正弦值为$\frac{\sqrt{5}-1}{2}$.分析 根据三角形三边关系判断得到A为最小角,C为直角,利用勾股定理列出关系式,与已知等式联立求出$\frac{a}{c}$的值,即为sinA的最小值.
解答 解:∵一个直角三角形的三边长a<b<c,
∴C为直角,A为最小角,
∴sinA的最小值为$\frac{a}{c}$,
∵$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}={c}^{2}}\\{{b}^{2}=ac}\end{array}\right.$,
∴a2+ac=c2,即$\frac{{a}^{2}}{{c}^{2}}$+$\frac{a}{c}$=1,
解得:$\frac{a}{c}$=$\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 此题考查了余弦定理,勾股定理,以及三角形三边关系,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
9.设等差数列{an}满足:cos2a3cos2a5-sin2a3sin2a5-cos2a3=sin(a1+a7),a4≠$\frac{kπ}{2}$,k∈Z且公差d∈(-1,0),若当且仅当n=8时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| A. | [$\frac{3π}{2}$,2π] | B. | ($\frac{3π}{2}$,2π) | C. | [$\frac{7π}{4}$,2π] | D. | ($\frac{7π}{4}$,2π) |
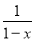 ∈M,则当4∈M时,集合M的所有元素之积等于( )
∈M,则当4∈M时,集合M的所有元素之积等于( )