题目内容
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
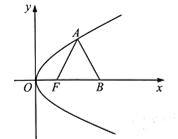
(Ⅱ)设经过点F的直线交椭圆C于M,N两点,线段MN的垂直平分线交y轴于点P(0,y0),求y0的取值范围.
【答案】(1)![]() +
+![]() =1. (2)
=1. (2)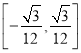
【解析】
试题解:(Ⅰ)设椭圆C的半焦距是c.依题意,得c=1.
因为椭圆C的离心率为![]() ,
,
所以a=2c=2,b2=a2-c2=3.
故椭圆C的方程为![]() +
+![]() =1.
=1.
(Ⅱ)当MN⊥x轴时,显然y0=0.
当MN与x轴不垂直时,可设直线MN的方程为
y=k(x-1)(k≠0).
由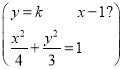
消去y并整理得(3+4k2)x2-8k2x+4(k2-3)=0.
设M(x1,y1),N(x2,y2),线段MN的中点为Q(x3,y3),
则x1+x2=![]() .
.
所以x3=![]() =
=![]() ,y3=k(x3-1)=
,y3=k(x3-1)=![]() .
.
线段MN的垂直平分线的方程为
y+![]() =-
=-![]()
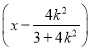 .
.
在上述方程中,令x=0,得y0=![]() =
=![]() .
.
当k<0时,![]() +4k≤-4
+4k≤-4![]() ;当k>0时,
;当k>0时,![]() +4k≥4
+4k≥4![]() .
.
所以-![]() ≤y0<0或0<y0≤
≤y0<0或0<y0≤![]() .
.
综上,y0的取值范围是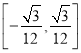 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目